题目内容
【题目】如图,在Rt△ABC中,∠BAC=90°,AD是BC边上的中线,过点D作BA的平行线交AC于点O,过点A作BC的平行线交DO的延长线于点E,连接CE.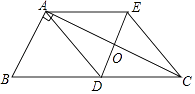
(1)求证:四边形ADCE是菱形;
(2)作出△ABC外接圆,不写作法,请指出圆心与半径;
(3)若AO:BD= ![]() :2,求证:点E在△ABC的外接圆上.
:2,求证:点E在△ABC的外接圆上.
【答案】
(1)证明:∵DE∥AB,AE∥BC,
∴四边形ADCE是平行四边形,
∵∠BAC=90°,AD是BC边上的中线,
∴AD= ![]() BC=CD,
BC=CD,
∴四边形ADCE是菱形
(2)解:如图所示:圆心为点D,AD、BD、CD都为半径
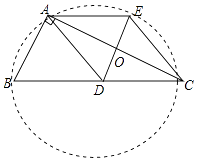
(3)证明:∵四边形ADCE是菱形,
∴AC⊥DE,OD=OE,
∴∠AOD=90°,
∵AO:BD=3:2,
∴AO:AD=3:2,
即sin∠ADO=3:2,
∴∠ADO=60°,
∴∠OAD=30°,
∴AD=2OD,
∴DE=DA,
∴点E在△ABC的外接圆上
【解析】(1)先证ABDE是平行四边形,得到AE=BD=CD,又AE∥BC,得出四边形ADCE是平行四边形,再利用斜边性质得AD=CD,证出菱形;(3)要证点E在△ABC的外接圆上,须证DE=DA,可转化DE=AB,利用AO:BD= ![]() :2,可得sin∠ADO=
:2,可得sin∠ADO=![]() :2,所以∠ADO=60°,∠OAD=30°,AD=2OD,进而DE=DA.
:2,所以∠ADO=60°,∠OAD=30°,AD=2OD,进而DE=DA.
【考点精析】关于本题考查的三角形的外接圆与外心和切线的性质定理,需要了解过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能得出正确答案.

练习册系列答案
相关题目