题目内容
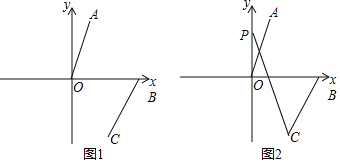
【题目】如图，一次函数y=﹣ 
x+m（m＞0）的图象与x轴、y轴分别交于点A，B，点C在线段OA上，点C的横坐标为n，点D在线段AB上，且AD=2BD，将△ACD绕点D旋转180°后得到△A1C1D．
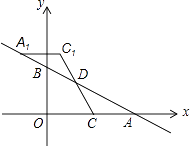
（1）若点C1恰好落在y轴上，试求 
的值；
（2）当n=4时，若△A1C1D被y轴分得两部分图形的面积比为3：5，求该一次函数的解析式．
【答案】
（1）解：由题意，得B（0，m），A（2m，0），
如图，过点D作x轴的垂线，交x轴于点E，交直线A1C1于点F，
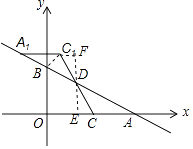
易知：DE= 
m，D（ m， m），C1（ 
m﹣n， m），
∴ m﹣n=0，∴ 
=
（2）解：由（1）得，当m＞3时，点C1在y轴右侧；当2＜m＜3时，点C1在y轴左侧．
①当m＞3时，设A1C1与y轴交于点P，连接C1B，
由△A1C1D被y轴分得两部分图形的面积比为3：5，∴S△BA1P：S△BC1P=3：1，
∴A1P：C1P=3，∴ m=3（ m﹣4），∴m= 
，
∴y=﹣ 
x+ 
；
②当2＜m＜3时，同理可得：y=﹣ x+ ；
综上所述，y=﹣ x+ 或y=﹣ x+ ．
【解析】（1）由旋转的性质可得AC1=AC，AD=A1D，当C1落在y轴上时，可得相似，即
,对应边成比例，得出AC1=
n,即2m-n=m,得出
;（2）可分类讨论，m＞3时，C1在y轴右侧，可得出S△BA1P：S△BC1P=3：1，底边长比也为3：1，进而求出解析式；当2＜m＜3时，点C1在y轴左侧，类似的可求出解析式.
【考点精析】关于本题考查的确定一次函数的表达式和旋转的性质，需要了解确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法；①旋转后对应的线段长短不变，旋转角度大小不变；②旋转后对应的点到旋转到旋转中心的距离不变；③旋转后物体或图形不变，只是位置变了才能得出正确答案．
