ЬтФПФкШн
ЁОЬтФПЁП![]() БэЪОвд
БэЪОвд![]() ЮЊздБфСПЕФКЏЪ§ЃЌдђ
ЮЊздБфСПЕФКЏЪ§ЃЌдђ![]() БэЪОЕБ
БэЪОЕБ![]() ЪБ
ЪБ![]() КЏЪ§ЕФжЕЃЎР§ШчЃЌвЛДЮКЏЪ§
КЏЪ§ЕФжЕЃЎР§ШчЃЌвЛДЮКЏЪ§![]() МЧзї
МЧзї![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌКЏЪ§жЕ
ЪБЃЌКЏЪ§жЕ![]() ЃЎЯжИјГіаТЖЈвхЃКЖдгкКЏЪ§
ЃЎЯжИјГіаТЖЈвхЃКЖдгкКЏЪ§![]() ЃЌШєДцдкЪЕЪ§
ЃЌШєДцдкЪЕЪ§![]() ЃЌЪЙЕУГЩСЂ
ЃЌЪЙЕУГЩСЂ![]() ЃЌдђГЦЕу
ЃЌдђГЦЕу![]() ЪЧКЏЪ§
ЪЧКЏЪ§![]() ЕФЁАЦцУюЕуЁБЃЎ
ЕФЁАЦцУюЕуЁБЃЎ
ЃЈ1ЃЉЧѓКЏЪ§![]() ЕФЁАЦцУюЕуЁБЃЛ
ЕФЁАЦцУюЕуЁБЃЛ
ЃЈ2ЃЉЕБ![]() ЮЊКЮжЕЪБЃЌКЏЪ§
ЮЊКЮжЕЪБЃЌКЏЪ§![]() ДцдкЁАЦцУюЕуЁБЃП
ДцдкЁАЦцУюЕуЁБЃП
ЃЈ3ЃЉШєЖўДЮКЏЪ§![]() гаЧвжЛгавЛИіЁАЦцУюЕуЁБ
гаЧвжЛгавЛИіЁАЦцУюЕуЁБ![]() ЃЌЦфЭМЯѓгы
ЃЌЦфЭМЯѓгы![]() жсНЛгк
жсНЛгк![]() СНЕуЃЈЕу
СНЕуЃЈЕу![]() дкЕу
дкЕу![]() ЕФзѓВрЃЉЃЌ
ЕФзѓВрЃЉЃЌ![]() ЪЧ
ЪЧ![]() жсЩЯвЛЖЏЕуЃЎЕБ
жсЩЯвЛЖЏЕуЃЎЕБ![]() ЕФжмГЄзюЖЬЪБЃЌЧѓЕу
ЕФжмГЄзюЖЬЪБЃЌЧѓЕу![]() ЕФзјБъМА
ЕФзјБъМА![]() ЕФжмГЄЃЎ
ЕФжмГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЪЧКЏЪ§
ЪЧКЏЪ§![]() ЕФЁАЦцУюЕуЁБЃЛЃЈ2ЃЉ
ЕФЁАЦцУюЕуЁБЃЛЃЈ2ЃЉ![]() ЮЊШЮвтЪЕЪ§ЪБЛђ
ЮЊШЮвтЪЕЪ§ЪБЛђ![]() ЪБЃЛЃЈ3ЃЉ
ЪБЃЛЃЈ3ЃЉ![]() ЕФжмГЄЮЊ
ЕФжмГЄЮЊ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЬтвтЕУЃК4x+6ЃН2x+12ЃЌЧѓГіxЃН3ЃЌдђД№АИПЩЧѓГіЃЛ
ЃЈ2ЃЉЗжШ§жжВЛЭЌЧщПіЬжТлЃКЂйЕБ2aЉ2Ёй0ЃЌМДaЁй1ЃЌbЮЊШЮвтЪЕЪ§ЪБЃЌКЏЪ§yЃН2ax+3bЉ2гавЛИіЁАЦцУюЕуЁБЃЛЂкЕБ2aЉ2ЃН0Чв14Љ3bЃН0ЃЌМДaЃН1ЃЌbЃН![]() ЪБЃЌКЏЪ§yЃН2ax+3bЉ2гаЮоЪ§ИіЁАЦцУюЕуЁБЃЛЂлЕБ2aЉ2ЃН0Чв14Љ3bЁй0ЃЌМДaЃН1ЃЌbЁй
ЪБЃЌКЏЪ§yЃН2ax+3bЉ2гаЮоЪ§ИіЁАЦцУюЕуЁБЃЛЂлЕБ2aЉ2ЃН0Чв14Љ3bЁй0ЃЌМДaЃН1ЃЌbЁй![]() ЪБЃЌКЏЪ§yЃН2ax+3bЉ2УЛгаЁАЦцУюЕуЁБЃЎ
ЪБЃЌКЏЪ§yЃН2ax+3bЉ2УЛгаЁАЦцУюЕуЁБЃЎ
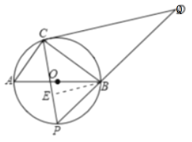
ЃЈ3ЃЉгЩЬтвтЕУЗНГЬax2Љ2x+8ЃН2x+12гаЧвжЛгавЛИіНтЃЌЧѓГіAЕузјБъЃЌПЩЕУЖўДЮКЏЪ§yЃНЉx2Љ2x+8ЕФЭМЯѓгыxжсЕФНЛЕуЮЊBЃЈЉ4ЃЌ0ЃЉЃЌCЃЈ2ЃЌ0ЃЉЃЎШчЭМЃЌзїЕуBЙигкyжсЕФЖдГЦЕуB'ЃЌСЌНгB'AНЛyжсгкЕуPЃЌдђPЕуЮЊЫљЧѓЃЌЧѓГіжБЯпB'AЕФНтЮіЪНЮЊ![]() ЃЌдђЕуPЕФзјБъПЩЧѓГіЃЌЧѓГіABКЭAB'ЕФГЄМДПЩЕУГіД№АИЃЎ
ЃЌдђЕуPЕФзјБъПЩЧѓГіЃЌЧѓГіABКЭAB'ЕФГЄМДПЩЕУГіД№АИЃЎ
НтЃКЃЈ1ЃЉгЩЬтвтЕУЃК4x+6ЃН2x+12ЃЌ
НтЕУЃКxЃН3ЃЎ
ЁрЃЈ3ЃЌ18ЃЉЪЧКЏЪ§yЃН4x+6ЕФЦцУюЕуЃЛ
ЃЈ2ЃЉгЩ2ax+3bЉ2ЃН2x+12ЕУЃЈ2aЉ2ЃЉxЃН14Љ3bЃЌ
ЂйЕБ2aЉ2Ёй0ЃЌМДaЁй1ЃЌbЮЊШЮвтЪЕЪ§ЪБЃЌЗНГЬЃЈ2aЉ2ЃЉxЃН14Љ3bгаЮЈвЛНтxЃН![]() ЃЌКЏЪ§yЃН2ax+3bЉ2гавЛИіЁАЦцУюЕуЁБЃЛ
ЃЌКЏЪ§yЃН2ax+3bЉ2гавЛИіЁАЦцУюЕуЁБЃЛ
ЂкЕБ2aЉ2ЃН0Чв14Љ3bЃН0ЃЌМДaЃН1ЃЌbЃН![]() ЪБЃЌЗНГЬЃЈ2aЉ2ЃЉxЃН14Љ3bЕФНтЮЊШЋЬхЪЕЪ§ЃЌКЏЪ§yЃН2ax+3bЉ2гаЮоЪ§ИіЁАЦцУюЕуЁБЃЛ
ЪБЃЌЗНГЬЃЈ2aЉ2ЃЉxЃН14Љ3bЕФНтЮЊШЋЬхЪЕЪ§ЃЌКЏЪ§yЃН2ax+3bЉ2гаЮоЪ§ИіЁАЦцУюЕуЁБЃЛ
ЂлЕБ2aЉ2ЃН0Чв14Љ3bЁй0ЃЌМДaЃН1ЃЌbЁй![]() ЪБЃЌЗНГЬЃЈ2aЉ2ЃЉxЃН14Љ3bЮоНтЃЌКЏЪ§yЃН2ax+3bЉ2УЛгаЁАЦцУюЕуЁБЃЎ
ЪБЃЌЗНГЬЃЈ2aЉ2ЃЉxЃН14Љ3bЮоНтЃЌКЏЪ§yЃН2ax+3bЉ2УЛгаЁАЦцУюЕуЁБЃЎ
ЃЈ3ЃЉЁпЖўДЮКЏЪ§yЃНax2Љ2x+8ЃЈaЁй0ЃЉгаЧвжЛгавЛИіЁАЦцУюЕуЁБЃЌ
ЁрЗНГЬax2Љ2x+8ЃН2x+12гаЧвжЛгавЛИіНтЃЌ
ИУЗНГЬПЩЛЏЮЊax2Љ4xЉ4ЃН0ЃЌ
ЁрЁїЃНЃЈЉ4ЃЉ2Љ4ЁСЃЈЉ4aЃЉЃН0ЃЌ
НтЕУЃЌaЃНЉ1ЃЌ
ЁрyЃНЉx2Љ2x+8ЕФЁАЦцУюЕуЁБЮЊAЃЈЉ2ЃЌ8ЃЉЃЌ
ЁрЖўДЮКЏЪ§ЕФНтЮіЪНЮЊyЃНЉx2Љ2x+8ЃЌ
ЁрЖўДЮКЏЪ§yЃНЉx2Љ2x+8ЕФЭМЯѓгыxжсЕФНЛЕуЮЊBЃЈЉ4ЃЌ0ЃЉЃЌCЃЈ2ЃЌ0ЃЉЃЎ
ШчЭМЃЌзїЕуBЙигкyжсЕФЖдГЦЕуB'ЃЌСЌНгB'AНЛyжсгкЕуPЃЌдђPЕуЮЊЫљЧѓЃЌ
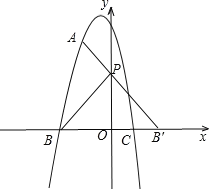
ЧѓЕУB'ЃЈ4ЃЌ0ЃЉЃЌ
ЩшжБЯпжБЯпB'AЕФНтЮіЪНЮЊyЃНkx+bЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУЃК ЃЌ
ЃЌ
ЁржБЯпB'AЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
ЁрPЃЈ0ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁрЁїPABЕФжмГЄЮЊ![]() ЃЎ
ЃЎ