题目内容
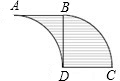
如图,正方形纸片ABCD中,E为BC的中点,折叠正方形,使点A与点E重合,压平后,得折痕MN,设梯形ADMN的面积为S,梯形BCMN的面积是T,求S:T的值.


连接MA,ME,
由翻折可得,AN=NE,AM=ME,
设AB=2x,AN=a,在Rt△BEN中,a2=(2x-a)2+x2,4xa=5x2,a=
x,
∴在Rt△ADM,设DM=b,Rt△ADM中,AM2=(2x)2+b2,
在Rt△EMC中,CM=2x-b,
(2x-b)2+x2=(2x)2+b2,
则DM=b=
x,
∴
=
=
=
.

由翻折可得,AN=NE,AM=ME,
设AB=2x,AN=a,在Rt△BEN中,a2=(2x-a)2+x2,4xa=5x2,a=
| 5 |
| 4 |
∴在Rt△ADM,设DM=b,Rt△ADM中,AM2=(2x)2+b2,
在Rt△EMC中,CM=2x-b,
(2x-b)2+x2=(2x)2+b2,
则DM=b=
| 1 |
| 4 |
∴
| S |
| T |
| DM+AN |
| BN+CM |
| ||||
|
| 3 |
| 5 |


练习册系列答案
相关题目