题目内容
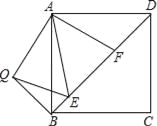
【题目】如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证:
(1)EA是∠QED的平分线;
(2)EF2=BE2+DF2.

【答案】详见解析.
【解析】试题分析:(1)、直接利用旋转的性质得出△AQE≌△AFE(SAS),进而得出∠AEQ=∠AEF,即可得出答案;(2)、利用(1)中所求,再结合勾股定理得出答案.
试题解析:(1)、∵将△ADF绕点A顺时针旋转90°后,得到△ABQ, ∴QB=DF,AQ=AF,∠ABQ=∠ADF=45°,
∴△AQE≌△AFE(SAS), ∴∠AEQ=∠AEF, ∴EA是∠QED的平分线;
(2)、由(1)得△AQE≌△AFE, ∴QE=EF, 在Rt△QBE中,
QB2+BE2=QE2, 则EF2=BE2+DF2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目