题目内容
【题目】在![]() 中,
中,![]() ,点
,点![]() 为射线
为射线![]() 上一个动点(不与
上一个动点(不与![]() 重合),以
重合),以![]() 为一边在
为一边在![]() 的右侧作
的右侧作![]() ,使
,使![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,连接
,连接![]() .
.
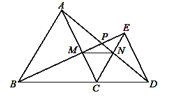
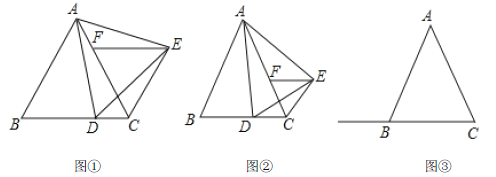
(1)如图①,若![]() ,则按边分类:
,则按边分类:![]() 是 三角形,并证明;
是 三角形,并证明;
(2)若![]() .
.
①如图②,当点![]() 在线段
在线段![]() 上移动时,判断
上移动时,判断![]() 的形状并证明;
的形状并证明;
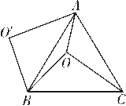
②当点![]() 在线段
在线段![]() 的延长线上移动时,
的延长线上移动时,![]() 是什么三角形?请在图③中画出相应的图形并直接写出结论(不必证明).
是什么三角形?请在图③中画出相应的图形并直接写出结论(不必证明).
【答案】(1)等边;证明见解析;(2)①△EFC为等腰三角形,证明见解析;②△EFC为等腰三角形.
【解析】
(1)根据题意推出∠ACB=∠ABC=60°,然后通过求证△EAC≌△DAB,结合平行线的性质,即可推出△EFC为等边三角形;
(2)①根据(1)的推理方法,即可推出△EFC为等腰三角形;②根据题意画出图形,然后根据平行线的性质,通过求证△EAC≌△DAB,推出等量关系,即可推出△EFC为等腰三角形.
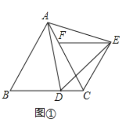
解:(1)如图1,∵AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠ACB=∠ABC=60°,∠EAC=∠DAB,
∴△DAB≌△EAC,
∴∠ECA=∠B=60°,
∵EF∥BC,
∴∠EFC=∠ACB=60°,
∵在△EFC中,∠EFC=∠ECF=60°=∠CEF,
∴△EFC为等边三角形,
故答案为:等边;
(2)①△CEF为等腰三角形,
证明:如图2,∵AB=AC,AD=AE,∠BAC=∠DAE,
∴∠ACB=∠ABC,∠EAC=∠DAB,
∴△EAC≌△DAB,
∴∠ECA=∠B,
∴∠ACE=∠ACB,
∵EF∥BC,
∴∠EFC=∠ACB,
∴∠EFC=∠ACE,
∴CE=FE,
∴△EFC为等腰三角形;

②如图③,△EFC为等腰三角形.
当点D在BC延长线上时,以AD为一边在AD的左侧作△ADE,使AD=AE,∠DAE=∠BAC,过点E作BC的平行线EF,交直线AC的延长线于点F,连接DE.
证明:∵AB=AC,AD=AE,∠BAC=∠DAE,
∴∠ACB=∠ABC,∠EAC=∠DAB,
∴△EAC≌△DAB,
∴∠ECA=∠DBA,
∴∠ECF=∠ABC,
∵EF∥BC,
∴∠AFE=∠ACB,
又∵∠ABC=∠ACB,
∴∠AFE=∠ECF,
∴EC=EF,
∴△EFC为等腰三角形.