��Ŀ����
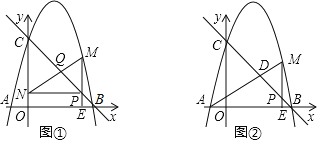
����Ŀ����ƽ��ֱ������ϵ�У���ABC��������������ֱ���A����1��1����B����4��1����C����3��3��.
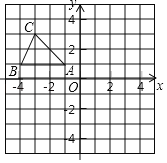
��1������ABC����ƽ��5����λ���Ⱥ�õ���A1B1C1���뻭����A1B1C1�����ж���O��A1��BΪ����������ε���״��ֱ��д���������
��2������ABC��ԭ��O˳ʱ����ת90���õ���A2B2C2���뻭����A2B2C2���������C��ת��C2��������·������
���𰸡���1����ͼ����A1B1C1Ϊ����������������O��A1��BΪ�����������Ϊ����ֱ�������Σ���2����ͼ����A2B2C2Ϊ����������������C��ת��C2��������·����Ϊ![]() ����
����
��������
��1�����õ�ƽ�Ƶ�����任����д��A1��B1��C1�����꣬����㼴�ɵõ���A1B1C1��Ȼ�����ù��ɶ������涨���ж���O��A1��BΪ����������ε���״��
��2�����������ص����ת�����ʻ���A��B��C�Ķ�Ӧ��A2��B2��C2���Ӷ����õ���A2B2C2��Ȼ�����û�����ʽ�������C��ת��C2��������·������
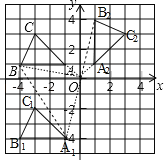
��1����ͼ����A1B1C1Ϊ������
��![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��
����O��A1��BΪ�����������Ϊ����ֱ�������Σ�
��2����ͼ����A2B2C2Ϊ��������C��ת��C2��������·����![]() ��
��