题目内容
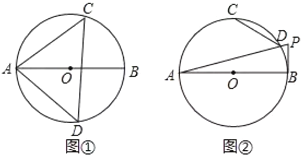
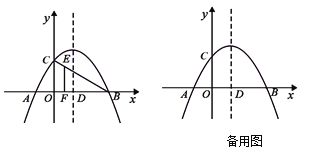
【题目】如图,直线y=﹣x+4与x轴交于点B,与y轴交于点C,抛物线y=﹣x2+bx+c经过B,C两点,与x轴另一交点为A.点P以每秒![]() 个单位长度的速度在线段BC上由点B向点C运动(点P不与点B和点C重合),设运动时间为t秒,过点P作x轴垂线交x轴于点E,交抛物线于点M.
个单位长度的速度在线段BC上由点B向点C运动(点P不与点B和点C重合),设运动时间为t秒,过点P作x轴垂线交x轴于点E,交抛物线于点M.
(1)求抛物线的解析式;
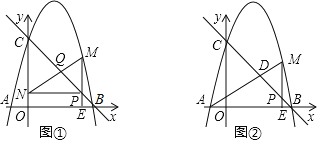
(2)如图①,过点P作y轴垂线交y轴于点N,连接MN交BC于点Q,当![]() 时,求t的值;
时,求t的值;
(3)如图②,连接AM交BC于点D,当△PDM是等腰三角形时,直接写出t的值.
【答案】(1)y=﹣x2+3x+4;(2)t的值为![]() ;(3)当△PDM是等腰三角形时,t=1或t=
;(3)当△PDM是等腰三角形时,t=1或t=![]() ﹣1.
﹣1.
【解析】
(1)求直线y=-x+4与x轴交点B,与y轴交点C,用待定系数法即求得抛物线解析式.
(2)根据点B、C坐标求得∠OBC=45°,又PE⊥x轴于点E,得到△PEB是等腰直角三角形,由![]() t求得BE=PE=t,即可用t表示各线段,得到点M的横坐标,进而用m表示点M纵坐标,求得MP的长.根据MP∥CN可证
t求得BE=PE=t,即可用t表示各线段,得到点M的横坐标,进而用m表示点M纵坐标,求得MP的长.根据MP∥CN可证![]() ,故有
,故有![]() ,把用t表示的MP、NC代入即得到关于t的方程,求解即得到t的值.
,把用t表示的MP、NC代入即得到关于t的方程,求解即得到t的值.
(3)因为不确定等腰△PDM的底和腰,故需分3种情况讨论:①若MD=MP,则∠MDP=∠MPD=45°,故有∠DMP=90°,不合题意;②若DM=DP,则∠DMP=∠MPD=45°,进而得AE=ME,把含t的式子代入并解方程即可;③若MP=DP,则∠PMD=∠PDM,由对顶角相等和两直线平行内错角相等可得∠CFD=∠PMD=∠PDM=∠CDF进而得CF=CD.用t表示M的坐标,求直线AM解析式,求得AM与y轴交点F的坐标,即能用t表示CF的长.把直线AM与直线BC解析式联立方程组,解得x的值即为点D横坐标.过D作y轴垂线段DG,得等腰直角△CDG,用DG即点D横坐标,进而可用t表示CD的长.把含t的式子代入CF=CD,解方程即得到t的值.
(1)直线y=﹣x+4中,当x=0时,y=4
∴C(0,4)
当y=﹣x+4=0时,解得:x=4
∴B(4,0)
∵抛物线y=﹣x2+bx+c经过B,C两点
∴![]() 解得:
解得:![]()
∴抛物线解析式为y=﹣x2+3x+4
(2)∵B(4,0),C(0,4),∠BOC=90°
∴OB=OC
∴∠OBC=∠OCB=45°
∵ME⊥x轴于点E,PB=![]() t
t
∴∠BEP=90°
∴Rt△BEP中,![]()
∴![]() ,
,
∴![]()
∵点M在抛物线上
∴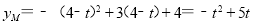 ,
,
∴![]() ,
,
∵PN⊥y轴于点N
∴∠PNO=∠NOE=∠PEO=90°
∴四边形ONPE是矩形
∴ON=PE=t
∴NC=OC﹣ON=4﹣t
∵MP∥CN
∴△MPQ∽△NCQ
∴![]()
∴![]()
解得:![]() (点P不与点C重合,故舍去)
(点P不与点C重合,故舍去)
∴t的值为![]()
(3)∵∠PEB=90°,BE=PE
∴∠BPE=∠PBE=45°
∴∠MPD=∠BPE=45°
①若MD=MP,则∠MDP=∠MPD=45°
∴∠DMP=90°,即DM∥x轴,与题意矛盾
②若DM=DP,则∠DMP=∠MPD=45°
∵∠AEM=90°
∴AE=ME
∵y=﹣x2+3x+4=0时,解得:x1=﹣1,x2=4
∴A(﹣1,0)
∵由(2)得,xM=4﹣t,ME=yM=﹣t2+5t
∴AE=4﹣t﹣(﹣1)=5﹣t
∴5﹣t=﹣t2+5t
解得:t1=1,t2=5(0<t<4,舍去)
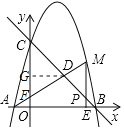
③若MP=DP,则∠PMD=∠PDM
如图,记AM与y轴交点为F,过点D作DG⊥y轴于点G
∴∠CFD=∠PMD=∠PDM=∠CDF
∴CF=CD
∵A(﹣1,0),M(4﹣t,﹣t2+5t),设直线AM解析式为y=ax+m
∴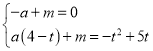 解得:
解得:![]() ,
,
∴直线AM:![]()
∴F(0,t)
∴CF=OC﹣OF=4﹣t
∵tx+t=﹣x+4,解得:![]() ,
,
∴![]() ,
,
∵∠CGD=90°,∠DCG=45°
∴![]() ,
,
∴![]()
解得:![]()
综上所述,当△PDM是等腰三角形时,t=1或![]() .
.

 阅读快车系列答案
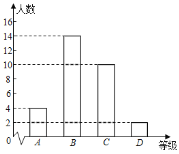
阅读快车系列答案【题目】九(1)班40名学生共分为4个学习小组,数学课代表制作了1~3组学生的期中考试数学成绩频数分布表和频数分布直方图如下.余下的第4小组10名学生成绩尚未统计,这10名学生成绩如下:60,65,72,75,75,75,86,86,96,99.
1~3组频数分布表
等级 | 分数段 | 频数(人数) |
D | 60≤x<70 | 2 |
C | 70≤x<80 | 10 |
B | 80≤x<90 | 14 |
A | 90≤x<100 | 4 |
根据以上信息,解答下列问题:
(1)求第4小组10名学生成绩的众数;
(2)请你仿照数学课代表制作全班1~4组频数分布表和频数分布直方图;
1~4组频数分布表
等级 | 分数段 | 频数(人数) |
D | 60≤x<70 |
|
C | 70≤x<80 |
|
B | 80≤x<90 |
|
A | 90≤x<100 |
|
(3)全校九年级共有600名学生参加期中考试,估计该校数学成绩为A等级的学生有多少人?