题目内容
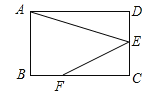
【题目】某广告公司设计一幅周长为16米的矩形广告牌,广告设计费为每平方米2000元.设矩形一边长为x,面积为S平方米.
(1)求S与x之间的函数关系式,并写出自变量x的取值范围;
(2)设计费能达到24000元吗?为什么?
(3)当x是多少米时,设计费最多?最多是多少元?
【答案】(1)![]() (0<x<8);(2)能;(3)当x=4米时,矩形的最大面积为16平方米,设计费最多,最多是32000元.
(0<x<8);(2)能;(3)当x=4米时,矩形的最大面积为16平方米,设计费最多,最多是32000元.
【解析】
试题分析:(1)由矩形的一边长为x、周长为16得出另一边长为8﹣x,根据矩形的面积公式可得答案;
(2)由设计费为24000元得出矩形面积为12平方米,据此列出方程,解之求得x的值,从而得出答案;
(3)将函数解析式配方成顶点式,可得函数的最值情况.
试题解析:(1)∵矩形的一边为x米,周长为16米,∴另一边长为(8﹣x)米,∴S=x(8﹣x)=![]() ,其中0<x<8,即
,其中0<x<8,即![]() (0<x<8);
(0<x<8);
(2)能,∵设计费能达到24000元,∴当设计费为24000元时,面积为24000÷200=12(平方米),即![]() =12,解得:x=2或x=6,∴设计费能达到24000元.
=12,解得:x=2或x=6,∴设计费能达到24000元.
(3)∵![]() =
=![]() ,∴当x=4时,S最大值=16,∴当x=4米时,矩形的最大面积为16平方米,设计费最多,最多是32000元.
,∴当x=4时,S最大值=16,∴当x=4米时,矩形的最大面积为16平方米,设计费最多,最多是32000元.

【题目】为了进一步了解某校八年级学生的身体素质情况,体育老师对该校八年级(1)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,图表如下所示:
组别 | 次数x | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 | a |
第4组 | 140≤x<160 | 18 |
第5组 | 160≤x<180 | 6 |
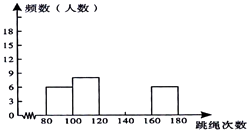
请结合图表完成下列问题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若在一分钟内跳绳次数少于120次的为测试不合格,则该校八年级共1000人中,一分钟跳绳
不合格的人数大约有多少?