题目内容
【题目】如图,在△ABC中,点P是BC边上任意一点(点P与点B,C不重合),平行四边形AFPE的顶点F,E分别在AB,AC上.已知BC=2,S△ABC=1.设BP=x,平行四边形AFPE的面积为y.
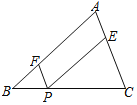
(1)求y与x的函数关系式;
(2)上述函数有最大值或最小值吗?若有,则当x取何值时,y有这样的值,并求出该值;若没有,请说明理由.
【答案】(1)y=-![]() x2+x;(2)当x=1时,y有最大值,最大值为
x2+x;(2)当x=1时,y有最大值,最大值为![]()
【解析】
(1)由平行四边形的性质得出PF∥CA,证出△BFP∽△BAC,得出面积比等于相似比的平方,得出S△BFP=![]() ,同理:S△PEC=(
,同理:S△PEC=(![]() )2,即可得出y与x的函数关系式;
)2,即可得出y与x的函数关系式;
(2)由![]() <0得出y有最大值,把(1)中函数关系式化成顶点式,即可得出结果.
<0得出y有最大值,把(1)中函数关系式化成顶点式,即可得出结果.
(1)∵四边形AFPE是平行四边形,
∴PF∥CA,∴△BFP∽△BAC,
∴![]() =(
=(![]() )2,
)2,
∵S△ABC=1,∴S△BFP=![]() ,
,
同理:S△PEC=(![]() )2=
)2=![]() ,
,
∴y=1-![]() -
-![]() ,
,
∴y=-![]() x2+x;
x2+x;
(2)上述函数有最大值,最大值为 ;理由如下:
∵y=-![]() x2+x =-
x2+x =-![]() (x﹣1)2+
(x﹣1)2+![]() ,又-
,又-![]() <0,
<0,
∴y有最大值,
∴当x=1时,y有最大值,最大值为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目