题目内容
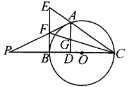
【题目】如图，在
中，
、
分别是
、
边上的高．求证：
．
【答案】见解析
【解析】
要证明
，这两个三角形已经有一个公共角相等，此时可以考虑用两组对应边的比相等且相应的夹角相等的两个三角形相似，即找到CD：CA与CE：CB是否相等，这时不能直接的找出，则充分利用题干“
、
分别是
、
边上的高”中的垂直关系找到角相等的关系，再证明△CDA∽△CEB得到CD：CE=CA：CB从而运用比例的基本性质得到CD：CA=CE：CB.
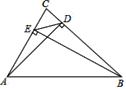
证明：∵在△ABC中，AD、BE分别是BC、AC边上的高
∴∠ADC=∠BEC=90°
∵∠C是公共角，∴△CDA∽△CEB（两组角对应相等的两个三角形相似）
∴CD：CE=CA：CB（相似三角形对应边成比例）
∴CD：CA=CE：CB（比例的基本性质）
∴△DCE∽△ACB．（两组对应边的比相等且相应的夹角相等的两个三角形相似）
练习册系列答案
相关题目
