题目内容
【题目】如图,在平面直角坐标系中,二次函数y=(x-a)(x-3)(0<a<3)的图象与x轴交于点A、B(点A在点B的左侧),与y轴交于点D,过其顶点C作直线CP⊥x轴,垂足为点P,连接AD、BC.
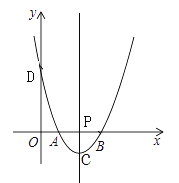
(1)求点A、B、D的坐标;
(2)若△AOD与△BPC相似,求a的值;
(3)点D、O、C、B能否在同一个圆上,若能,求出a的值,若不能,请说明理由.
【答案】(1)(1)A(a,0),B(3,0),D(0,3a).(2)a的值为![]() .(3)当a=
.(3)当a=![]() 时,D、O、C、B四点共圆.
时,D、O、C、B四点共圆.
【解析】(1)根据二次函数的图象与x轴相交,则y=0,得出A(a,0),B(3,0),与y轴相交,则x=0,得出D(0,3a).
(2)根据(1)中A、B、D的坐标,得出抛物线对称轴x=![]() ,AO=a,OD=3a,代入求得顶点C(
,AO=a,OD=3a,代入求得顶点C(![]() ,-
,-![]() ),从而得PB=3-
),从而得PB=3- ![]() =
=![]() ,PC=
,PC=![]() ;再分情况讨论:①当△AOD∽△BPC时,根据相似三角形性质得
;再分情况讨论:①当△AOD∽△BPC时,根据相似三角形性质得 ,解得:a=
,解得:a= ![]() 3(舍去);
3(舍去);
②△AOD∽△CPB,根据相似三角形性质得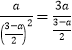 ,解得:a1=3(舍),a2=
,解得:a1=3(舍),a2=![]() ;
;
(3)能;连接BD,取BD中点M,根据已知得D、B、O在以BD为直径,M(![]() ,
,![]() a)为圆心的圆上,若点C也在此圆上,则MC=MB,根据两点间的距离公式得一个关于a的方程,解之即可得出答案.
a)为圆心的圆上,若点C也在此圆上,则MC=MB,根据两点间的距离公式得一个关于a的方程,解之即可得出答案.
(1)∵y=(x-a)(x-3)(0<a<3)与x轴交于点A、B(点A在点B的左侧),
∴A(a,0),B(3,0),
当x=0时,y=3a,
∴D(0,3a);
(2)∵A(a,0),B(3,0),D(0,3a).∴对称轴x=![]() ,AO=a,OD=3a,
,AO=a,OD=3a,
当x= ![]() 时,y=-
时,y=- ![]() ,
,
∴C(![]() ,-
,-![]() ),
),
∴PB=3-![]() =
=![]() ,PC=
,PC=![]() ,
,
①当△AOD∽△BPC时,
∴![]() ,
,
即  ,
,
解得:a= ![]() 3(舍去);
3(舍去);
②△AOD∽△CPB,
∴![]() ,
,
即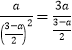 ,
,
解得:a1=3(舍),a2=![]() .
.
综上所述:a的值为![]() ;
;
(3)能;连接BD,取BD中点M,
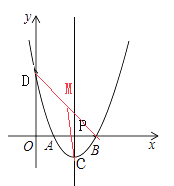
∵D、B、O三点共圆,且BD为直径,圆心为M(![]() ,
,![]() a),
a),
若点C也在此圆上,
∴MC=MB,
∴ ,
,
化简得:a4-14a2+45=0,
∴(a2-5)(a2-9)=0,
∴a2=5或a2=9,
∴a1=![]() ,a2=-
,a2=-![]() ,a3=3(舍),a4=-3(舍),
,a3=3(舍),a4=-3(舍),
∵0<a<3,
∴a=![]() ,
,
∴当a=![]() 时,D、O、C、B四点共圆.
时,D、O、C、B四点共圆.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案