题目内容
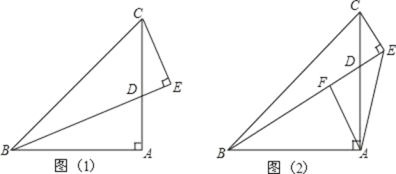
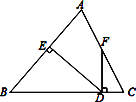
【题目】如图所示，△ABC中，AB=BC，DE⊥AB于点E，DF⊥BC于点D，交AC于F．
⑴若∠AFD=155°，求∠EDF的度数；
⑵若点F是AC的中点，求证：∠CFD=
∠B．
【答案】（1）50°；（2）见解析
【解析】试题分析：⑴根据等腰三角形的性质、三角形的内角和定理与四边形的内角和为360°，可求得所求角的度数.
⑵连接BF，根据三角形内角和定理与等腰三角形三线合一，可知
.
试题解析：⑴ ∵∠AFD=155°，∴∠DFC=25°，∵DF⊥BC，DE⊥AB，
∴∠FDC=∠AED=90°，
在Rt△EDC中，∴∠C=90°﹣25°=65°，
∵AB=BC，∴∠C=∠A=65°，
∴∠EDF=360°﹣65°﹣155°﹣90°=50°．
⑵ 连接BF，∵AB=BC，且点F是AC的中点，
∴BF⊥AC，
，
∴∠CFD+∠BFD=90°，∠CBF+∠BFD=90°，
∴∠CFD=∠CBF，
∴．
练习册系列答案
阅读快车系列答案
相关题目
