题目内容
【题目】四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,AB=7,
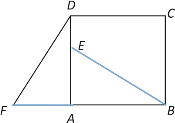
求:(1)指出旋转中心和旋转角度
(2)求DE的长度
(3)BE与DF的位置关系如何?并说明理由.
【答案】(1)旋转中心为点A,旋转角度为90°或270°;(2)3;(3)BE⊥DF,理由见解析.
【解析】
(1)根据旋转的性质可得△AFD≌△AEB,再根据全等三角形的性质可得AE=AF=4,∠EAF=90°,∠EBA=∠FDA,然后根据旋转的性质分顺时针和逆时针旋转两种情况解答;
(2)根据旋转的性质可得AE=AF,AD=AB,然后根据DE=AD-AE计算即可得解;
(3)根据旋转可得△ABE和△ADF全等,根据全等三角形对应边相等可得BE=DF,全等三角形对应角相等可得∠ABE=∠ADF,然后求出∠ABE+∠F=90°,判断出BE⊥DF.
(1) 根据旋转的性质可知:△AFD≌△AEB,
所以,AE=AF=4,∠EAF=90°,∠EBA=∠FDA,
可得旋转中心为点A,旋转角度为90°或270°;
(2)∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴AE=AF=4,AD=AB=7,
∴DE=ADAE=74=3;
(3)BE、DF的关系为: BE⊥DF.理由如下:
∵△ADF按顺时针方向旋转一定角度后得到△ABE,
∴△ABE≌△ADF,
∴BE=DF,∠ABE=∠ADF,
∵∠ADF+∠F=180°90°=90°,
∴∠ABE+∠F=90°,
∴BE⊥DF,
∴BE、DF的关系为:BE⊥DF.

练习册系列答案
相关题目