题目内容
【题目】已知抛物线![]() 与
与![]() 形状相同,开口方向不同,其中抛物线
形状相同,开口方向不同,其中抛物线![]() :
:![]() 交x轴于A,B两点
交x轴于A,B两点![]() 点A在点B的左侧
点A在点B的左侧![]() ,且
,且![]() ,抛物线
,抛物线![]() 与
与![]() 交于点A与
交于点A与![]() .
.
![]() 求抛物线
求抛物线![]() ,
,![]() 的函数表达式;
的函数表达式;
![]() 当x的取值范围是______时,抛物线
当x的取值范围是______时,抛物线![]() 与
与![]() 上的点的纵坐标同时随横坐标的增大而增大;
上的点的纵坐标同时随横坐标的增大而增大;
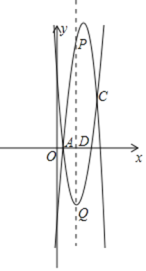
![]() 直线
直线![]() 轴,分别交x轴,
轴,分别交x轴,![]() ,
,![]() 于点
于点![]() ,P,Q,当
,P,Q,当![]() 时,求线段PQ的最大值.
时,求线段PQ的最大值.
【答案】![]() 的函数表达式为
的函数表达式为![]() ,
,![]() 的函数表达式为
的函数表达式为![]() ;
;![]() ;
;![]() 16.
16.
【解析】
![]() 利用二次函数图象上点的坐标特征可得出点A,B的横坐标,由
利用二次函数图象上点的坐标特征可得出点A,B的横坐标,由![]() 可得出关于a的方程,解之即可得出a的值,进而可得出抛物线
可得出关于a的方程,解之即可得出a的值,进而可得出抛物线![]() 的函数表达式,利用二次函数图象上点的坐标特征可得出点A,C的坐标,由点A,C的坐标,利用待定系数法即可求出抛物线
的函数表达式,利用二次函数图象上点的坐标特征可得出点A,C的坐标,由点A,C的坐标,利用待定系数法即可求出抛物线![]() 的函数表达式;
的函数表达式;
![]() 利用二次函数的性质分别找出抛物线
利用二次函数的性质分别找出抛物线![]() ,
,![]() 上点的纵坐标随横坐标的增大而增大的x的取值范围,取其公共部分即可得出结论;
上点的纵坐标随横坐标的增大而增大的x的取值范围,取其公共部分即可得出结论;
![]() 利用二次函数图象上点的坐标特征可得出点P,Q的坐标,进而可得出PQ的长度,分
利用二次函数图象上点的坐标特征可得出点P,Q的坐标,进而可得出PQ的长度,分![]() ,
,![]() 及
及![]() 三种情况找出PQ的最大值,取其中的最大值即可得出结论.
三种情况找出PQ的最大值,取其中的最大值即可得出结论.
解:![]() 当
当![]() 时,
时,![]() ,
,
解得:![]() ,
,![]() .
.![]() ,
,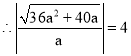 ,
,![]() ,
,![]() 抛物线
抛物线![]() 的函数表达式为
的函数表达式为![]() .
.
当![]() 时,
时,![]() ,
,
解得:![]() ,
,![]() ,
,![]() 点A的坐标为
点A的坐标为![]() ,点B的坐标为
,点B的坐标为![]() .
.
当![]() 时,
时,![]() ,
,![]() 点C的坐标为
点C的坐标为![]() .
.
设抛物线![]() 的函数表达式为
的函数表达式为![]() ,
,
将![]() ,
,![]() 代入
代入![]() ,得:
,得:![]() ,
,
解得:![]() ,
,![]() 抛物线
抛物线![]() 的函数表达式为
的函数表达式为![]() .
.
![]() 当
当![]() 时,抛物线
时,抛物线![]() 上的点的纵坐标随横坐标的增大而增大,
上的点的纵坐标随横坐标的增大而增大,
当![]() 时,抛物线
时,抛物线![]() 上的点的纵坐标随横坐标的增大而增大.
上的点的纵坐标随横坐标的增大而增大.![]() 当
当![]() 时,抛物线
时,抛物线![]() 与
与![]() 上的点的纵坐标同时随横坐标的增大而增大.
上的点的纵坐标同时随横坐标的增大而增大.
故答案为:![]() .
.![]() 点P的坐标为
点P的坐标为![]() ,
,![]() 点P的坐标为
点P的坐标为![]() ,点Q的坐标为
,点Q的坐标为![]() ,
,![]() .
.![]() 当
当![]() 时,
时,![]() ,
,![]() ,
,![]() 随着n的增大而减小,
随着n的增大而减小,![]() 当
当![]() 时,PQ取得最大值,最大值为7;
时,PQ取得最大值,最大值为7;![]() 时,
时,![]() ,
,![]() ,
,![]() 当
当![]() 时,PQ取得最大值,最大值为9;
时,PQ取得最大值,最大值为9;![]() 当
当![]() 时,
时,![]() ,
,![]() ,
,![]() 随着n的增大而增大,
随着n的增大而增大,![]() 当
当![]() 时,PQ取得最大值,最大值为16.
时,PQ取得最大值,最大值为16.
综上所述:当![]() 时,线段PQ的最大值为16.
时,线段PQ的最大值为16.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
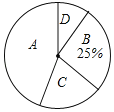
名师点睛字词句段篇系列答案【题目】某校开设了“3D”打印、数学史、诗歌欣赏、陶艺制作四门校本课程,为了解学生对这四门校本课程的喜爱情况,对学生进行了随机问卷调査(问卷调査表如图所示),将调査结果整理后绘制例图1、图2两幅均不完整的统计图表.
最受欢迎的校本课程调查问卷
您好!这是一份关于您最喜欢的校本课程问卷调查表,请在表格中选择一个(只能选一个)您最喜欢的课程选项,在其后空格内打“√”,非常感谢您的合作.
选项 | 校本课程 | |
A | 3D打印 | |
B | 数学史 | |
C | 诗歌欣赏 | |
D | 陶艺制作 |
校本课程 | 频数 | 频率 |
A | 36 | 0.45 |
B | 0.25 | |
C | 16 | b |
D | 8 | |
合计 | a | 1 |
请您根据图表中提供的信息回答下列问题:
(1)统计表中的a= ,b= ;
(2)“D”对应扇形的圆心角为 度;
(3)根据调査结果,请您估计该校2000名学生中最喜欢“数学史”校本课程的人数;
(4)小明和小亮参加校本课程学习,若每人从“A”、“B”、“C”三门校本课程中随机选取一门,请用画树状图或列表格的方法,求两人恰好选中同一门校本课程的概率.