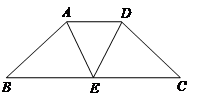题目内容
矩形纸片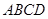 的边长
的边长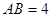 ,
,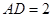 。将矩形纸片沿
。将矩形纸片沿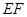 折叠,使点
折叠,使点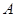 与点
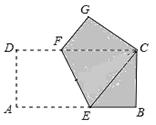
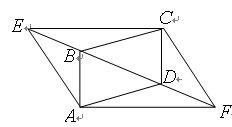
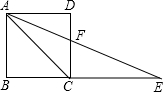
与点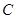 重合,折叠后在其一面着色(如图所示),则着色部分的部分面积为
重合,折叠后在其一面着色(如图所示),则着色部分的部分面积为
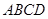 的边长
的边长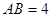 ,
,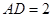 。将矩形纸片沿
。将矩形纸片沿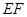 折叠,使点
折叠,使点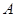 与点
与点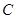 重合,折叠后在其一面着色(如图所示),则着色部分的部分面积为
重合,折叠后在其一面着色(如图所示),则着色部分的部分面积为 
A. | B. | C. | D. |
B
试题分析:设BE=x,则AE=EC=CF=4-x,在Rt△ECB中,CE2=BE2+BC2,∴(4-x)2=x2+22,∴x=
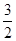 ,CF=
,CF=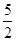 .
.S着色部分=S矩形ABCD-S△ECF=4×2-
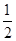 ×
×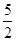 ×2=
×2=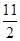
点评:解题过程中使用翻折变换,可保留原有图形的性质,且使原来分散条件相对集中,以利于问题的解决。

练习册系列答案
相关题目
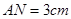 ,长
,长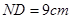 ,
,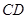 上的点
上的点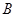 距地面的高
距地面的高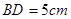 ,地面上
,地面上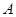 处的一只蚂蚁要到
处的一只蚂蚁要到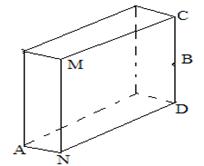
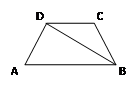
 中,
中, 为底
为底 的中点,连结
的中点,连结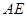 、
、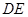 .
.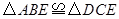 .
.