题目内容
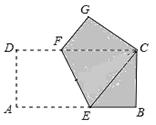
如图所示，在正方形ABCD的边BC的延长线上取一点E，使CE=CA，连接AE交CD于F，则∠AFD=_________。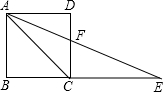
67.5°，
试题分析：由图知∠AFD=∠FAC+∠ACF，即求出∠FAC，∠ACF的值，可知∠AFD的度数．
∵ABCD为正方形
∴DC⊥BC
即∠DCE=90°
又∵AC是正方形ABCD的对角线
∴∠ACF=45°
∴∠ACE=∠DCE+∠ACF=135°
∵CE=CA
∴∠FAC=∠E=
（180°-135°）=22.5°∴∠AFD=∠FAC+∠ACF=22.5°+45°=67.5°．
点评：解答和正方形有关的题目，要充分利用正方形的对角线平分每一组对角，且解答时要注意45°角的特殊作用．
练习册系列答案
阅读快车系列答案
相关题目
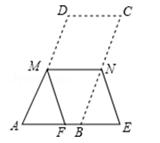
自B→A→E→B停止，点Q自D→F→C→D停止，点P运动的路程是m，点Q运动的路程是n，当四边形BPDQ是平行四边形时，求m与n满足的数量关系．(画出示意图)
ABCD的一边长为10，则对角线AC、BD的长可取下列数据中的（ ）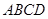
的边长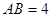
，
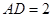。将矩形纸片沿
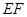折叠，使点
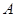与点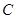
重合，折叠后在其一面着色（如图所示），则着色部分的部分面积为 
