题目内容
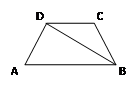
在等腰梯形ABCD中,AB∥CD,DC =" 3" cm,∠A=60°,BD平分∠ABC,则这个梯形的周长是( )

| A.21 cm; | B.18 cm; | C.15cm; | D.12 cm; |
C
试题分析:根据题意,可知∠A=∠ABC=60°,即可推出∠ABD=∠DBC=30°,∠ADB=90°,∠BDC=30°,因此,CD=BC=AD=3,根据含30°角的直角三角形的性质可知AB=6,便可推出梯形的周长.
∵等腰梯形ABCD中,AB∥CD,DC=3cm,∠A=60°,
∴BC=AD,∠A=∠ABC=60°,
∵BD平分∠ABC,
∴∠ABD=∠DBC=30°,
∴∠BDC=30°,
∵∠ABD=30°,∠A=60°,
∴∠ADB=90°,
∵CD=3cm,
∴CD=BC=AD=3,
∴AB=2AD=6,
∴梯形ABCD的周长=AB+BC+CD+DA=6+3+3+3=15cm.
故选择C.
点评:解答本题的关键是熟练掌握含30°角的直角三角形的性质:直角三角形中30°角所对的直角边等于斜边的一半.

练习册系列答案
相关题目
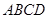 沿
沿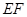 ,
,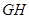 同时折叠,
同时折叠,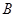 、
、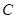 两点恰好都落在
两点恰好都落在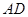 边的
边的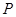 点处,若
点处,若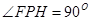 ,
,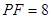 ,
,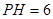 ,则长方形
,则长方形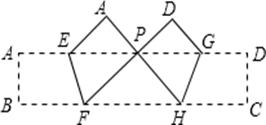
 ABCD的一边长为10,则对角线AC、BD的长可取下列数据中的( )
ABCD的一边长为10,则对角线AC、BD的长可取下列数据中的( )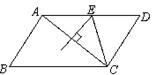
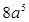 ,其中一条边长为
,其中一条边长为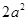 ,则另一条边长为 ___________。
,则另一条边长为 ___________。 的边长
的边长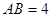 ,
,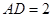 。将矩形纸片沿
。将矩形纸片沿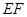 折叠,使点
折叠,使点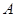 与点
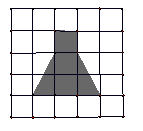
与点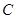 重合,折叠后在其一面着色(如图所示),则着色部分的部分面积为
重合,折叠后在其一面着色(如图所示),则着色部分的部分面积为