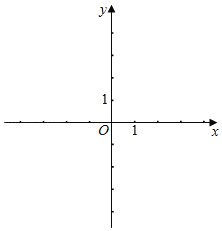题目内容
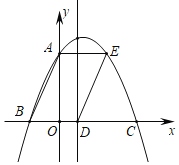
【题目】如图，抛物线y＝ax2+bx+
与y轴交于点A，与x轴交于点B、C，连结AB，以AB为边向右做平行四边形ABDE，点E落在抛物线上，点D落在x轴上，若抛物线的对称轴恰好经过点D，且∠ABD＝60°，则平行四边形的面积为_____．
【答案】
．
【解析】
根据题意，可以求得点A的坐标，然后根据平行四边形的性质和二次函数的性质，可以求得OA和BD的长，从而可以求得平行四边形ABDE的面积．
∵抛物线y=ax2+bx+
与y轴交于点A，
∴点A的坐标为（0，），
又∵四边形ABDE是平行四边形，点D在抛物线的对称轴上，点A和点E关于对称轴对称，
∴BD=AE=2OB，
∵OA=，∠ABD=60°，∠AOB=90°，
∴OB=1，
∴BD=2，
∴平行四边形的面积为：2×=2，
故答案为：2．
练习册系列答案
作业辅导系列答案
相关题目
