题目内容
【题目】如图,∠BAD=90°,AB=AD,CB=CD,一个以点C为顶点的45°角绕点C旋转,角的两边与BA,DA交于点M,N,与BA,DA的延长线交于点E,F,连接AC.
(1)在∠FCE旋转的过程中,当∠FCA=∠ECA时,如图1,求证:AE=AF;
(2)在∠FCE旋转的过程中,当∠FCA≠∠ECA时,如图2,如果∠B=30°,CB=2,用等式表示线段AE,AF之间的数量关系,并证明.

【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)先证明△ABC≌△ADC,然后再证明△ACF≌△ACE即可得;
(2)过点C作CG⊥AB于点G,先求出AC的长,再证明△ACF∽△AEC,根据相似三角形的性质即可得.
试题解析:(1)∵AB=AD,BC=CD,AC=AC,∴△ABC≌△ADC,
∴∠BAC=∠DAC=45°,∴180°-∠BAC=180°-∠DAC,∴∠FAC=∠EAC=135°,
又∵∠FCA=∠ECA,
∴△ACF≌△ACE,
∴AE=AF;
(2)过点C作CG⊥AB于点G,则∠BGC=∠AGC=90°,
∵∠B=30°,∴CG=![]() BC=
BC=![]() =1,
=1,
∵∠BAC=45°,∴AC=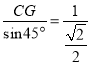 =
=![]() ,
,
∵∠FAC=∠EAC=135°,∴∠ACF+∠F=45°,
又∵∠ACF+∠ACE=45°,∴∠F=∠ACE,
∴△ACF∽△AEC,
∴![]() ,即
,即![]() ,
,
∴![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目