Question

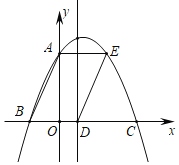
【题目】我们把一条抛物线上横坐标与纵坐标相等的点叫做这条抛物线的“不动点”．如图，在平面直角坐标系xOy中，已知抛物线y＝x2﹣2x，其顶点为A．

（1）试求抛物线y＝x2﹣2x的“不动点”的坐标；

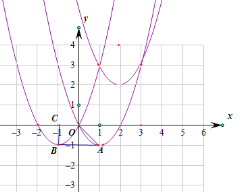
（2）平移抛物线y＝x2﹣2x，使所得新抛物线的顶点B是该抛物线的“不动点”，其对称轴与x轴交于点C，且四边形OABC是梯形，求新抛物线的表达式．

Answer 1

【答案】（1）抛物线的“不动点”为（0，0），（3，3）；（2）新抛物线的解析式为y＝x2+2x

【解析】

（1）设抛物线y＝x2﹣2x的“不动点”的坐标（t，t），则t＝t2﹣2t，求得t＝0或t＝3；

（2）OC∥AB时，设B（m，m），则新抛物线的对称轴为x＝m，与x轴的交点C（m，0），当OC∥AB，由A（1，﹣1），B（m，m），可求m＝﹣1，故新抛物线是抛物线y＝x2﹣2x向左平移2个单位得到的；当OB∥AC时，同理可得：抛物线解析式y＝﹣（x﹣2）2+2＝x2﹣4x+6，当四边形OABC是梯形，字母顺序不对，故舍去；

解：（1）设抛物线y＝x2﹣2x的“不动点”的坐标（t，t），

则t＝t2﹣2t，

∴t＝0或t＝3，

∴抛物线的“不动点”为（0，0），（3，3）；

（2）当OC∥AB时，

∵新抛物线顶点B为“不动点”，则设点B（m，m），

∴新抛物线的对称轴为：x=m，与x轴的交点C（m，0），

∵四边形OABC是梯形，

∴直线x=m在y轴左侧，

∵BC与OA不平行，

∴OC∥AB，

又∵点A（1，-1），点B（m，m），

∴m=-1，

故新抛物线是由抛物线y=x2-2x向左平移2个单位得到的，

∵原抛物线y＝x2﹣2x=（x-1）2-1，

∴平移后的抛物线为：y=（x+1）2-1=x2+2x；

当OB∥AC时，

同理可得：抛物线的表达式为：y=（x-2）2+2=x2-4x+6，

当四边形OABC是梯形，字母顺序不对，故舍去，

综上，新抛物线的表达式为：y= x2+2x．

综上所述：新抛物线的解析式为y＝x2+2x．