题目内容
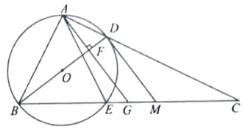
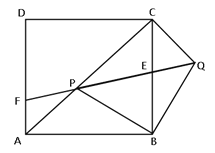
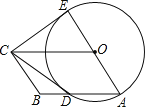
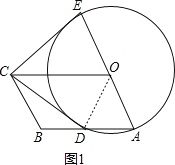
【题目】如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,
(1)求证:CD是⊙O的切线;
(2)若BC=3,AB=5,求平行四边形OABC的面积.
【答案】(1)见解析;(2)12
【解析】
(1)连接OD,证出△EOC≌△DOC,推出∠ODC=∠OEC=90°,根据切线的判定推出即可;
(2)求出CD,根据三角形的面积公式求出DF,根据平行四边形的面积公式求出即可.
∵CE是⊙O的切线,
∴∠OEC=90°,
连接OD,如图1,
∵四边形OABC是平行四边形,
∴AO=BC,OC=AB,OC∥AB,
∴∠EOC=∠A,∠COD=∠ODA,
∵OD=OA,
∴∠A=∠ODA,
∴∠EOC=∠DOC,
在△EOC和△DOC中,
∵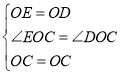 ,
,
∴△EOC≌△DOC(SAS),
∴∠ODC=∠OEC=90°,
∴OD⊥CD,
∴CD是⊙O的切线;
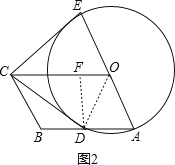
(2)过D作DF⊥OC于F,如图2,
∵四边形OABC是平行四边形,
∴OC=AB=5,OA=BC=3,
在Rt△CDO中,OC=5,OD=OA=3,
∴CD=![]() =4,
=4,
∵![]() ×CD×OD=
×CD×OD=![]() ×OC×DF,
×OC×DF,
∴DF=![]() =
=![]() ,
,
∴平行四边形OABC的面积=OC×DF=5×![]() =12.
=12.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】在不透明的袋子中有四张标有数字1,2,3,4的卡片,小明、小华两人按照各自的规则玩抽卡片游戏。
小明画出树形图如下:

小华列出表格如下:
第一次 第二次 | 1 | 2 | 3 | 4 |
1 | (1,1) | (2,1) | (3,1) | (4,1) |
2 | (1,2) | (2,2) | ① | (4,2) |
3 | (1,3) | (2,3) | (3,3) | (4,3) |
4 | (1,4) | (2,4) | (3,4) | (4,4) |
回答下列问题:
(1)根据小明画出的树形图分析,他的游戏规则是:随机抽出一张卡片后 (填“放回”或“不放回”),再随机抽出一张卡片;
(2)根据小华的游戏规则,表格中①表示的有序数对为 ;
(3)规定两次抽到的数字之和为奇数的获胜,你认为淮获胜的可能性大?为什么?