��Ŀ����
����Ŀ����֪������![]() ��
��![]() ��
��![]() �dz�������
�dz�������![]() ����������
����������![]() ��
��![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() .
.
�����������ߵĽ���ʽ��
��������![]() ������
������![]() ��һ�㣬����
��һ�㣬����![]() ��
��![]() ��Ĵ��ߣ�����Ϊ��
��Ĵ��ߣ�����Ϊ��![]() �����������ڵ�
�����������ڵ�![]() ����
����![]() �������Ϊ
�������Ϊ![]() ���߶�
���߶�![]() �ij�Ϊ
�ij�Ϊ![]() �����
�����![]() ��
��![]() ֮��ĺ�����ϵʽ����д����Ӧ���Ա���
֮��ĺ�����ϵʽ����д����Ӧ���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�����ڣ��������£�����![]() ���߶�
���߶�![]() ��ʱ����
��ʱ����![]() ����֪
����֪![]() ��
��![]() ����
����![]() Ϊδ֪����һԪ���η���
Ϊδ֪����һԪ���η���![]() ��
��![]() Ϊ������������ʵ��������
Ϊ������������ʵ��������![]() ���������ϣ�����
���������ϣ�����![]() ��
��![]() ��
��![]() ����
����![]() ƽ��
ƽ��![]() �����
�����![]() ֵ����
ֵ����![]() ������.
������.
���𰸡�����![]() ������
������![]() ��
��![]() ������
������![]() ֵΪ
ֵΪ![]() ��
��![]() ������Ϊ
������Ϊ![]() ��
��![]() .
.
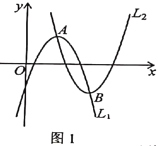
��������
������A![]() �͵�B��3��0���������y=a
�͵�B��3��0���������y=a![]() +bx+3�õ�a��b�ķ����飬Ȼ��ⷽ�����a��b�����ɵõ������ߵĽ���ʽ��
+bx+3�õ�a��b�ķ����飬Ȼ��ⷽ�����a��b�����ɵõ������ߵĽ���ʽ��
�����ȸ��ݴ���ϵ�������ֱ��BC�Ľ���ʽ���ֵ���P���߶�CB��ʱ���͵�P������BN��ʱ������������ۣ�![]() ��ĺ�����Ϊ
��ĺ�����Ϊ![]() ���ó�P�������Ϊ��t��-t+3����Q�������Ϊ��t��-t2+2t+3�����Ϳ��Եó�d��t֮��ĺ�����ϵʽ���ó����ۣ�
���ó�P�������Ϊ��t��-t+3����Q�������Ϊ��t��-t2+2t+3�����Ϳ��Եó�d��t֮��ĺ�����ϵʽ���ó����ۣ�
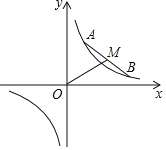
�����ݸ����б�ʽ�Ϳ������m��ֵ���Ϳ���������̵Ľ�����PQ��PH��ֵ���ӳ�MP��L��ʹLP=MP������LQ��LH���ӳ�MP��L��ʹLP=MP������LQ��LH���Ϳ��Եó��ı���LQMH��ƽ���ı��Σ������ó��ı���LQMH�����Σ������ε����ʾͿ���������ۣ�
�⣺����![]() ����
����![]() ��
��
��![]() ���
���![]()
�������ߵĽ���ʽΪ![]() ��
��
����![]() �������Ϊ
�������Ϊ![]() ��
��
��ֱ��![]() �ķ���Ϊ
�ķ���Ϊ![]() ��
��
��![]() ���룬��
���룬��![]() .
.
���![]() .
.
��ֱ��![]() �ķ���Ϊ
�ķ���Ϊ![]() .
.
��![]() ��ĺ�����Ϊ
��ĺ�����Ϊ![]() ����
����![]() ��ֱ��
��ֱ��![]() �ᣬ
�ᣬ
��![]() �������Ϊ
�������Ϊ![]() ��
��![]() �������Ϊ
�������Ϊ![]() .
.
����ͼ������![]() ���߶�
���߶�![]() ��ʱ��
��ʱ��
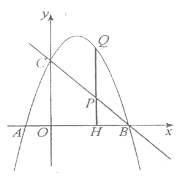
![]() .
.
����ͼ������![]() ������
������![]() ��ʱ��
��ʱ��

![]() .
.
��![]() ��
��
��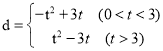
����![]() ��
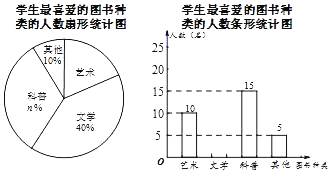
��![]() ������ʵ����.
������ʵ����.
��![]() ����
����![]() .
.
�����ã�![]() .
.
��![]() .
.
��![]() .
.
���Ϊ![]() .
.
���![]() .
.
��![]() ��
��![]() ��
��![]() ������ʵ������
������ʵ������
����![]() .
.
��![]() .
.
��![]() .
.
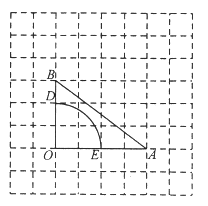
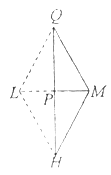
��ͼ���ӳ�![]() ��
��![]() ��ʹ
��ʹ![]() ������
������![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
���ı���![]() ��ƽ���ı���.
��ƽ���ı���.
��![]() .
.
��![]() .
.
��![]() ��
��
��![]() .
.
��![]() .
.
��![]() ������.
������.
��![]() .
.
���![]() �����������
�����������![]() ��������ȣ�����
��������ȣ�����![]() .
.
��![]() ����
�У���![]() ʱ��
ʱ��![]() .
.
��![]() .
.
���![]() .
.
����������![]() ֵΪ
ֵΪ![]() ��
��![]() ������Ϊ
������Ϊ![]() ��
��![]() .
.

 ȫ�ܲ��һ���þ�ϵ�д�
ȫ�ܲ��һ���þ�ϵ�д�