题目内容
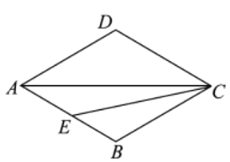
【题目】阅读材料:若抛物线![]() 的顶点
的顶点![]() 在抛物线
在抛物线![]() 上,抛物线
上,抛物线![]() 的顶点
的顶点![]() 也在抛物线
也在抛物线![]() 上(点
上(点![]() 与点
与点![]() 不重合),我们称这样的两条抛物线
不重合),我们称这样的两条抛物线![]() 、
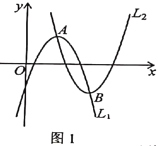
、![]() 互为“友好”抛物线,如图1.
互为“友好”抛物线,如图1.
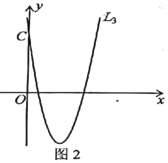
解决问题:如图2,已知物线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)若点![]() 与点
与点![]() 关于抛物线
关于抛物线![]() 的对称轴对称,求点
的对称轴对称,求点![]() 的坐标;
的坐标;
(2)求出以点![]() 为顶点的
为顶点的![]() 的“友好”抛物线
的“友好”抛物线![]() 的解析式;
的解析式;
(3)直接写出![]() 与
与![]() 中
中![]() 同时随
同时随![]() 增大而增大的自变量
增大而增大的自变量![]() 的取值范围.
的取值范围.
【答案】(1)点D坐标为(4,4)
(2)抛物线![]() 的解析式为
的解析式为![]()
(3)![]()
【解析】
(1)根据抛物线![]() 的解析式可求得C点坐标及对称轴,即可求得点D坐标.
的解析式可求得C点坐标及对称轴,即可求得点D坐标.
(2)可设![]() 的交点式解析式,将顶点坐标代入即可求解.
的交点式解析式,将顶点坐标代入即可求解.
(3)画图像,根据图像可得![]() 与
与![]() 中
中![]() 同时随
同时随![]() 增大而增大的自变量
增大而增大的自变量![]() 的取值范围.
的取值范围.
解:(1)∵点C是![]() 与
与![]() 轴交点
轴交点
∴点C坐标为(0,4)
将![]() 化成顶点式得:
化成顶点式得:![]()
∴顶点坐标为(2,-4),对称轴为![]()
∵点![]() 与点
与点![]() 关于抛物线
关于抛物线![]() 的对称轴对称
的对称轴对称
∴点D坐标为(4,4).
(2)设![]() 解析式为:
解析式为:![]()
将(2,-4)代入解得![]()
∴![]() 的“友好”抛物线
的“友好”抛物线![]() 的解析式为
的解析式为![]() .
.
(3)画出![]() 的图像.
的图像.

由图像可知当![]() 时,
时,![]() 与
与![]() 中
中![]() 同时随
同时随![]() 增大而增大.
增大而增大.
故答案为:(1)点D坐标为(4,4)
(2)抛物线![]() 的解析式为
的解析式为![]()
(3)![]()

 名校课堂系列答案
名校课堂系列答案【题目】某超市要进一批鸡蛋进行销售,有![]() 、
、![]() 两家农场可供货.为了比较两家提供的鸡蛋单个大小,超市分别对这两家农场的鸡蛋进行抽样检测,通过分析数据确定鸡蛋的供货商.
两家农场可供货.为了比较两家提供的鸡蛋单个大小,超市分别对这两家农场的鸡蛋进行抽样检测,通过分析数据确定鸡蛋的供货商.
(1)下列抽样方式比较合理的是哪一种?请简述原因.
①分别从![]() 、
、![]() 两家提供的一箱鸡蛋中拿出最上面的两层(共40枚)鸡蛋,并分别称出其中每一个鸡蛋的质量.
两家提供的一箱鸡蛋中拿出最上面的两层(共40枚)鸡蛋,并分别称出其中每一个鸡蛋的质量.
②分别从![]() 、
、![]() 两家提供的一箱鸡蛋中每一层随机抽4枚(共40枚)鸡蛋,并分别称出其中每个鸡蛋的质量.
两家提供的一箱鸡蛋中每一层随机抽4枚(共40枚)鸡蛋,并分别称出其中每个鸡蛋的质量.
(2)在用合理的方法抽出两家提供的鸡蛋各40枚后,分别称出每个鸡蛋的质量(单位:![]() ),结果如表所示(数据包括左端点不包括右端点).
),结果如表所示(数据包括左端点不包括右端点).
45~47 | 47~49 | 49~51 | 51~53 | 53~55 | |
| 2 | 8 | 15 | 10 | 5 |
| 4 | 6 | 12 | 14 | 4 |
①如果从这两家农场提供的鸡蛋中随机拿一个,分别估计两家鸡蛋质量在![]() (单位:
(单位:![]() )范围内的概率(数据包括左端点不包括右端点);
)范围内的概率(数据包括左端点不包括右端点);
②如果你是超市经营者,试通过数据分析确定选择哪家农场提供的鸡蛋.