题目内容
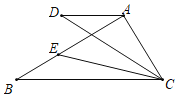
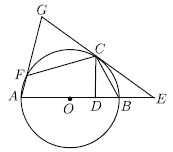
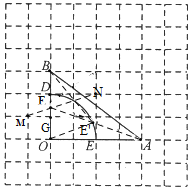
【题目】如图，在每个小正方形的边长为
的网格中，
的顶点
均在格点上，点
在
上，且点也在格点上.
（Ⅰ）
的值为_____________；
（Ⅱ）
是以点
为圆心，
为半径的一段圆弧.在如图所示的网格中，将线段
绕点逆时针旋转得到
，旋转角为，连接
，
，当
的值最小时，请用无刻度的直尺画出点
，并简要说明点的位置是如何找到的（不要求证明）______.
【答案】（Ⅰ）
（Ⅱ）取格点
，连接
，交
于点
；连接
，交
于点
，点即为所求.
【解析】
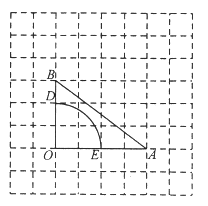
（Ⅰ）根据网格中OB和OE的长直接得出比值即可
（Ⅱ）取格点
，连接
，交
于点
；连接
，交
于点
，点即为所求.
解：（Ⅰ）∵由图可得OB=3，OE=2
∴
；
故答案为：
（Ⅱ）取格点，连接，交于点；连接，交于点，点即为所求.
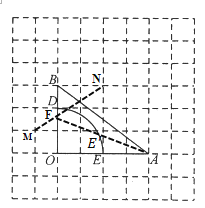
说明：线段
绕点
逆时针旋转得到
，则
，
连接
并延长交OB于点F，则
的值最小，要使
的值最小，需让
，即
，连接
,
,此时若△FOE′∽△E′OB，可得
，
则只需OF=
，需GF=
，只需将线段DG分为2:1即可，∴取DN=2，GM=1MN 交OB于点F连接AF交 于点..
【题目】为弘扬传统文化，某校开展了“传承经典文化，阅读经典名著”活动．为了解七、八年级学生(七、八年级各有600名学生)的阅读效果，该校举行了经典文化知识竞赛．现从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析，过程如下：
收集数据：
七年级：79，85，73，80，75，76，87，70，75，94，75，79，81，71，75，80，86，59，83，77．
八年级：92，74，87，82，72，81，94，83，77，83，80，81，71，81，72，77，82，80，70，41．
整理数据：
|
|
|
|
|
| |
七年级 | 0 | 1 | 0 | a | 7 | 1 |
八年级 | 1 | 0 | 0 | 7 | b | 2 |
分析数据：
平均数 | 众数 | 中位数 | |
七年级 | 78 | 75 |
|
八年级 | 78 |
| 80.5 |
应用数据：
(1)由上表填空：a= ，b= ，c= ，d= ．
(2)估计该校七、八两个年级学生在本次竞赛中成绩在90分以上的共有多少人？
(3)你认为哪个年级的学生对经典文化知识掌握的总体水平较好，请说明理由．
