题目内容
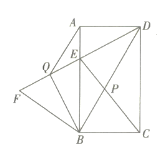
【题目】如图，在△ABC中，D、F分别是BC、AC边的中点，连接DA、DF，且AD＝2DF，过点B作AD的平行线交FD的延长线于点E．
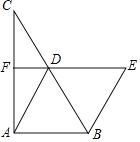
（1）求证：四边形ABED为菱形；
（2）若BD＝6，∠E＝60°，求四边形ABEF的面积．
【答案】(1)详见解析;(2) 
【解析】
（1）由三角形中位线定理得出DF∥AB，DF=
AB，证出四边形ABED是平行四边形，证出AD=AB，得出四边形ABED为菱形；
（2）过B作BG⊥EF于G，由菱形的性质得出AB=BE=DE=BD=6，得出DF=3，EF=9，证出△BDE是等边三角形，得出DG=DE=3，故BG=
DG=3，由梯形面积公式即可得出结果．
（1）证明：在△ABC中，D、F分别是BC、AC边的中点，
∴DF是△ABC的中位线，
∴DF∥AB，DF
AB，
∵BE∥AD，
∴四边形ABED是平行四边形，
∵AD＝2DF，
∴AD＝AB，
∴四边形ABED为菱形；
（2）过B作BG⊥EF于G，
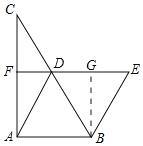
∵四边形ABED为菱形，
∴AB＝BE＝DE＝AD＝6，
∴DF＝3，EF＝9，
∵∠E＝60°，
∴△BDE是等边三角形，
∵BG⊥EF，
∴DGDE＝3，
∴BG
DG＝3，
∴四边形ABEF的面积
．
【题目】某超市要进一批鸡蛋进行销售，有
、
两家农场可供货．为了比较两家提供的鸡蛋单个大小，超市分别对这两家农场的鸡蛋进行抽样检测，通过分析数据确定鸡蛋的供货商．
（1）下列抽样方式比较合理的是哪一种？请简述原因．
①分别从、两家提供的一箱鸡蛋中拿出最上面的两层（共40枚）鸡蛋，并分别称出其中每一个鸡蛋的质量．
②分别从、两家提供的一箱鸡蛋中每一层随机抽4枚（共40枚）鸡蛋，并分别称出其中每个鸡蛋的质量．
（2）在用合理的方法抽出两家提供的鸡蛋各40枚后，分别称出每个鸡蛋的质量（单位：
），结果如表所示（数据包括左端点不包括右端点）．
45～47 | 47～49 | 49～51 | 51～53 | 53～55 | |
| 2 | 8 | 15 | 10 | 5 |
| 4 | 6 | 12 | 14 | 4 |
①如果从这两家农场提供的鸡蛋中随机拿一个，分别估计两家鸡蛋质量在
（单位：）范围内的概率（数据包括左端点不包括右端点）；
②如果你是超市经营者，试通过数据分析确定选择哪家农场提供的鸡蛋．
