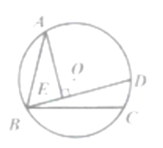题目内容
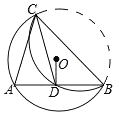
【题目】小明在学习“圆的对称性”时知道结论:垂直于弦的直径一定平分这条弦,请尝试解决问题:如图,在Rt△ACB中,∠ACB=90°,圆O是△ACB的外接圆.点D是圆O上一点,过点D作DE⊥BC,垂足为E,且BD平分∠ABE,
(1)判断直线ED与圆O的位置关系,并说明理由.
(2)若AC=12,BC=5,求线段BE的长.
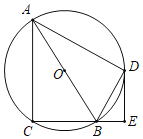
【答案】(1)直线ED与⊙O相切,见解析;(2)4
【解析】
(1)直线ED与⊙O相切.连接OD.根据圆的性质和等边对等角可得∠ODB=∠OBD,等量代换得到∠ODB=∠DBE,根据平行线的判定和性质得到∠DEC=∠ODE=90°,再根据垂直的定义和性质可得OD⊥DE,根据切线的判定即可求解;
(2)如图,延长DO交AC于点H,连结CO,构建直角△ABC的中位线OH,运用三角形中位线定理和勾股定理分别求得OH=HO=![]() BC=
BC=![]() 、AB=13,结合图形找到相关线段间的和差关系求得线段BE的长度即可.
、AB=13,结合图形找到相关线段间的和差关系求得线段BE的长度即可.
(1)如图,连接OD.
∵OB=OD,
∴∠ODB=∠OBD,
又∵∠OBD=∠DBE,
∴∠ODB=∠DBE,
∴OD∥BE,
又∵DE⊥BC,
∴∠DEC=90°,
∴∠ODE=90°,
∴OD⊥DE,
又∵OD为半径,
∴直线ED与⊙O相切;
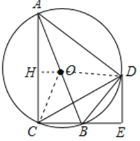
(2)如图,延长DO交AC于点H,连结CO,
∵OD∥BE,∠ODE=90°,
∴∠OHC=90°,即OH⊥AC,
又∵OA=OC,
∴AH=CH,又由O是AB的中点,
∴HO是△ABC的中位线,
∴HO=![]() BC=
BC=![]() .
.
∵AC为直径,
∴∠ACB=90°,
∴AC=12,BC=5,
∴AB=![]() =
=![]() =13,
=13,
∴OA=OD=![]() AB=
AB=![]() .
.
∴HD=HO+OD=9
由四边形CEDH是矩形,
∴CE=HD=9,
∴CE=9,
∴BE=CE﹣BC=4.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目