Question

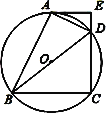
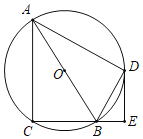
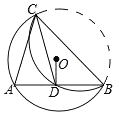
【题目】如图，在⊙O中，点C在优弧上，将沿BC折叠后刚好经过AB的中点D，连接AC，CD．则下列结论中错误的是（　　）

①AC＝CD；②AD＝BD；③+＝；④CD平分∠ACB

A.1B.2C.3D.4

Answer 1

【答案】A

【解析】

根据折叠的性质可得AD＝CD；根据线段中点的定义可得AD＝BD；根据垂径定理可作判断③；延长OD交⊙O于E，连接CE，根据垂径定理可作判断④．

过D作DD'⊥BC，交⊙O于D'，连接CD'、BD'，

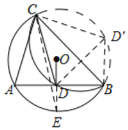
由折叠得：CD＝CD'，∠ABC＝∠CBD'，

∴AC＝CD'＝CD，

故①正确；

∵点D是AB的中点，

∴AD＝BD，

∵AC＝CD'，故②正确；

∴，

由折叠得：，

∴；

故③正确；

延长OD交⊙O于E，连接CE，

∵OD⊥AB，

∴∠ACE＝∠BCE，

∴CD不平分∠ACB，

故④错误；

故选：A．