Question

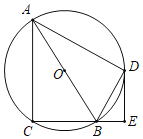
【题目】如图，⊙O的半径为1，弦AB=，BC=，AB，BC在圆心O的两侧，弧AC上有一动点D，AE⊥BD于点E，当点D从点C运动到点A时，则点E所经过的路径长为__________．

Answer 1

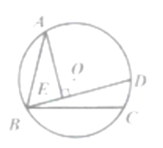
【答案】

【解析】

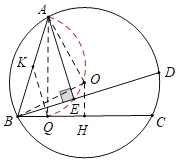
如图，连接OA，OB，作OH⊥BC于H，AQ⊥BC于Q，取AB的中点K，连接KQ．点E的运动轨迹是图中的红线，求出圆心角∠AKQ即可解决问题．

解：如图，连接OA，OB，作OH⊥BC于H，AQ⊥BC于Q，取AB的中点K，连接KQ．

∵OH⊥BC，

∴BH=CH=，

∴cos∠OBH=，

∴∠OBH=30°，

∵AB=，OA=OB=1，

∴AB2=OA2+OB2，

∴∠AOB=90°，

∴∠ABO=∠OAB=45°，

∴∠ABC=75°，

∵∠AQB=90°，AK=KB，

∴KB=KO，

∴∠KBQ=∠KQB=75°，

∴∠AKQ=∠KBQ+∠KQB=150°，

∵点E的运动轨迹是图中的红线，

∴点E所经过的路径长=．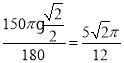
故答案为．