题目内容
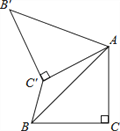
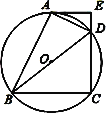
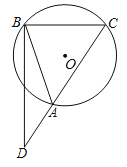
【题目】如图,⊙O的半径为2,弦AB的长为2![]() ,点C是优弧AB上的一动点,BD⊥BC交直线AC于点D,当点C从△ABC面积最大时运动到BC最长时,点D所经过的路径长为_____.
,点C是优弧AB上的一动点,BD⊥BC交直线AC于点D,当点C从△ABC面积最大时运动到BC最长时,点D所经过的路径长为_____.
【答案】![]() π
π
【解析】
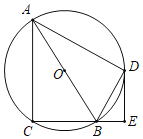
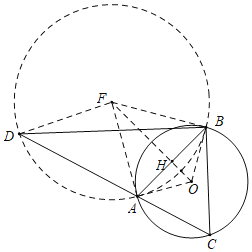
如图,以AB为边向上作等边三角形△ABF,连接OA,OB,OF,DF,OF交AB于H.说明点D的运动轨迹是以F为圆心,FA为半径的圆,再利用弧长公式求解即可.
如图,以AB为边向上作等边三角形△ABF,连接OA,OB,OF,DF,OF交AB于H.
∵FA=FB,OA=OB,
∴OF⊥AB,AH=BH=![]() ,
,
∴sin∠BOH=![]() ,
,
∴∠BOH=∠AOH=60°,
∴∠AOB=120°
∴∠C=![]() ∠AOB=60°,
∠AOB=60°,
∵DB⊥BC,
∴∠DBC=90°,
∴∠CDB=30°,
∵∠AFB=60°,
∴∠ADB=![]() ∠AFB,
∠AFB,
∴点D的运动轨迹是以F为圆心,FA为半径的圆,
∵当点C从△ABC面积最大时运动到BC最长时,BC绕点B顺时针旋转了30°,
∴BD绕点B也旋转了30°,
∴点D的轨迹所对的圆心角为60°,
∴运动路径的长![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目