题目内容
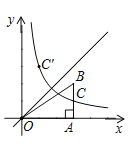
【题目】如图，点
，
在直线
上.抛物线
与线段
围成封闭图形
（包括边界），则内的整点（横、纵坐标都为整数）最多有（ ）
A.4个B.5个C.6个D.7个
【答案】C
【解析】
根据直线的解析式先判断出线段AB上的整数点个数，因为抛物线必过
，且抛物线要与
围成封闭图形
，则当
，图像过点
时，中的整数点最多；当
，图像过点
时，中的整数点最多，分别求出抛物线的解析式，再在网格图上画出图像，即可求出答案．
解：将A、B两点的纵坐标代入
可求得
，
，
把-5、-4、-3、-2、-1、0、1、2、3分别代入的x中，可得y的值分别为5、
、4、
、3、
、2、
、1，则线段上的整数点有
，
，
，
，
．
必过，且抛物线要与围成封闭图形，则
当，图像过点时，
，此时中的整数点最多；
当，图像过点时，
，此时中的整数点最多；
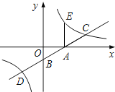
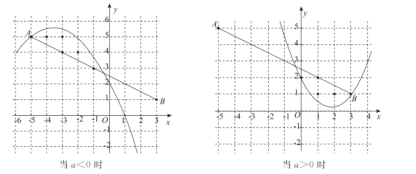
分别画出图像，根据整数刻度画出网格，如下图所示，
当，内的整数点共有6个，
当，内的整数点共有5个，
故内的整数点最多有6个．
故选：C．
练习册系列答案
一线名师提优试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
