题目内容
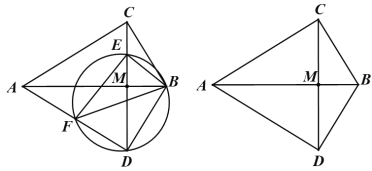
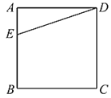
【题目】如图,在平面直角坐标系中,已知二次函数y=ax2+4ax+c(a<0)的图像与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为点D,DH⊥x轴于H与AC交于点E.连接CD、BC、BE.若S△CBE∶S△ABE=2∶3,
(1)点A的坐标为 ,点B的坐标为 ;
(2)连结BD,是否存在数值a,使得∠CDB=∠BAC?若存在,请求出a的值;若不存在,请说明理由;
(3)若AC恰好平分∠DCB,求二次函数的表达式.

【答案】(1) (-5,0);(1,0);(2)不存在;理由见解析;(3)y=-![]() x2-
x2-![]() x+
x+![]()
【解析】
(1)由![]() 可得
可得![]() ,即可求得
,即可求得![]() ,求出设直线EC的函数解析式为
,求出设直线EC的函数解析式为![]() ,求出A(-5,0),利用A、B关于抛物线对称轴对称即可得出B(1,0);
,求出A(-5,0),利用A、B关于抛物线对称轴对称即可得出B(1,0);
(2)求出OC=-5a,DH=-9a,可得tan∠BAC=![]() =-a,过点B作BF⊥BD交DC延长线于点F,过点F作FG⊥x轴于点G,由△BFG∽△DBH,利用相似三角性质可求得
=-a,过点B作BF⊥BD交DC延长线于点F,过点F作FG⊥x轴于点G,由△BFG∽△DBH,利用相似三角性质可求得![]() ,由
,由![]() ,求得a=0,故不存在;
,求得a=0,故不存在;
(3)连结AD,可得S△ACD=S△ABC,由AC平分∠DCB,可得CD=BC,列出方程,求得a=![]() ,即可得出答案.
,即可得出答案.
(1)∵y=ax2+4ax+c
∴抛物线的对称轴为x=-2
依题意得C(0,c)
∵![]()
∴![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
设直线EC的函数解析式为![]()
∴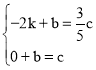
∴
∴![]()
当y=0时,![]()
∴x=-5
∴A(-5,0)
∵A、B关于直线x=-2对称
∴B(1,0)
故答案为:A(-5,0),B(1,0)
(2)将B(1,0)代入表达式得,c=-5a,
∴OC=-5a,DH=-9a
∴tan∠BAC=![]() =-a
=-a
过点B作BF⊥BD交DC延长线于点F,
过点F作FG⊥x轴于点G
△BFG∽△DBH
∴![]() =tan∠BAC
=tan∠BAC
=tan∠BAC=-a
∴![]()
∵![]() ,
,
∴![]() ,a=0,
,a=0,
∴不存在
(3)解:连结AD,EH=![]() OC=-3a,
OC=-3a,
∴S△ACD=![]() ·DE·(xC-xA) =-15a
·DE·(xC-xA) =-15a
S△ABC=![]() ·AB·OC =-15a,
·AB·OC =-15a,
∴S△ACD=S△ABC
∵AC平分∠DCB,
∴CD=BC
∴4+16a2=1+25a2
解得,a1=-![]() ,a2=
,a2=![]()
∵a<0,
∴a=![]()
∴y=-![]() x2-
x2-![]() x+
x+![]()


 名校课堂系列答案
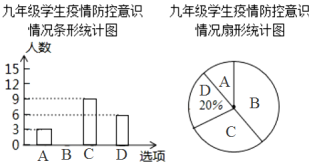
名校课堂系列答案【题目】疫情期间,“线上教学”为我们提供了复习的渠道.学校随机抽取部分学生就“你是否喜欢线上教学”进行了问卷调查,并将调查结果统计后绘制成如下统计表和统计图.
调查结果统计表
类别 | 非常喜欢 | 喜欢 | 一般 | 不喜欢 |
频数 | a | 70 | 20 | 10 |
频率 | 0.5 | b | 0.15 | |
调查结果扇形统计图

(1)在统计表中,a= ;b= ;
(2)在扇形统计图中,对线上教学感觉“一般”所对应的圆心角度数为 ;
(3)已知全校共有3000名学生,试估计“喜欢”线上教学的学生人数.