Question

【题目】如图1，已知△ABC中，AB=10cm，AC=8cm，BC=6cm．如果点P由B出发沿BA方向点A匀速运动，同时点Q由A出发沿AC方向向点C匀速运动，它们的速度均为2cm/s．连接PQ，设运动的时间为t（单位：s）（0≤t≤4）．解答下列问题：

（1）当t为何值时，PQ∥BC．

（2）设△AQP面积为S（单位：cm2），当t为何值时，S取得最大值，并求出最大值．

（3）是否存在某时刻t，使线段PQ恰好把△ABC的面积平分？若存在，求出此时t的值；若不存在，请说明理由．

（4）如图2，把△AQP沿AP翻折，得到四边形AQPQ′．那么是否存在某时刻t，使四边形AQPQ′为菱形？若存在，求出此时菱形的面积；若不存在，请说明理由．

Answer 1

【答案】（1）s（2）当t=s时，S取得最大值，最大值为cm2（3）不存在。理由见解析（4）存在，cm2

【解析】

解：∵AB=10cm，AC=8cm，BC=6cm，

∴由勾股定理逆定理得△ABC为直角三角形，∠C为直角。

（1）BP=2t，则AP=10﹣2t．

若PQ∥BC，则，即，解得。

∴当s时，PQ∥BC。

（2）如图1所示，过P点作PD⊥AC于点D。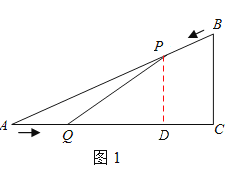

则PD∥BC，∴△APD∽△ABC。

∴，即，解得。

∴S=×AQ×PD=×2t×（）

。

∴当t=s时，S取得最大值，最大值为cm2。

（3）不存在。理由如下：

假设存在某时刻t，使线段PQ恰好把△ABC的面积平分，

则有S△AQP=S△ABC，而S△ABC=ACBC=24，∴此时S△AQP=12。

由（2）可知，S△AQP=，∴=12，化简得：t2﹣5t+10=0。

∵△=（﹣5）2﹣4×1×10=﹣15＜0，此方程无解，

∴不存在某时刻t，使线段PQ恰好把△ABC的面积平分。

（4）存在。

假设存在时刻t，使四边形AQPQ′为菱形，

则有AQ=PQ=BP=2t。

如图2所示，过P点作PD⊥AC于点D，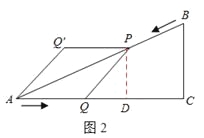

则有PD∥BC，

∴△APD∽△ABC。

∴，即。

解得：PD=，AD=，

∴QD=AD﹣AQ=。

在Rt△PQD中，由勾股定理得：QD2+PD2=PQ2，即（）2+（）2=（2t）2，

化简得：13t2﹣90t+125=0，解得：t1=5，t2=。

∵t=5s时，AQ=10cm＞AC，不符合题意，舍去，∴t=。

由（2）可知，S△AQP=

∴S菱形AQPQ′=2S△AQP=2×（）=2×[﹣×（）2+6×]=。

∴存在时刻t=，使四边形AQPQ′为菱形，此时菱形的面积为cm2。

（1）由PQ∥BC时的比例线段关系，列一元一次方程求解。

（2）如图1所示，过P点作PD⊥AC于点D，得△APD∽△ABC，由比例线段，求得PD，从而可以得到S的表达式，然后利用二次函数的极值求得S的最大值。

（3）利用（2）中求得的△AQP的面积表达式，再由线段PQ恰好把△ABC的面积平分，列出一元二次方程；由于此一元二次方程的判别式小于0，则可以得出结论：不存在这样的某时刻t，使线段PQ恰好把△ABC的面积平分。

（4）根据菱形的性质及相似三角形比例线段关系，求得PQ、QD和PD的长度；然后在Rt△PQD中，求得时间t的值；最后求菱形的面积，值得注意的是菱形的面积等于△AQP面积的2倍，从而可以利用（2）中△AQP面积的表达式，这样可以化简计算。