题目内容
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() (点
(点![]() 在点
在点![]() 左侧).直线
左侧).直线![]() 与抛物线的对称轴交于点
与抛物线的对称轴交于点![]() .
.
(1)求抛物线的对称轴;
(2)直接写出点![]() 的坐标;
的坐标;
(3)点![]() 与点
与点![]() 关于抛物线的对称轴对称,过点
关于抛物线的对称轴对称,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() 与直线
与直线![]() 交于点
交于点![]() ,若
,若![]() ,结合函数图象,求
,结合函数图象,求![]() 的取值范围.
的取值范围.
【答案】(1)抛物线的对称轴为直线![]() ;(2)点C的坐标为
;(2)点C的坐标为![]() ;(3)a的取值范围是
;(3)a的取值范围是![]() 或
或![]() .
.
【解析】
(1)将点![]() 代入
代入![]() ,求得
,求得![]() ,即为对称轴;
,即为对称轴;
(2)由(1)知对称轴![]() ,即
,即![]() ,得
,得![]() ,代入
,代入![]() ,令
,令![]() ,可解得C点坐标;
,可解得C点坐标;
(3)表示出点A,点M的坐标,根据![]() 轴,得
轴,得![]() ,表示出EN,进而得MN长度表示,用
,表示出EN,进而得MN长度表示,用![]() ,解出
,解出![]() 的取值范围即可.
的取值范围即可.
(1)![]() 直线
直线![]() 与抛物线的对称轴交于点
与抛物线的对称轴交于点![]() ,
,
![]() .
.
![]() 抛物线的对称轴为直线
抛物线的对称轴为直线![]() .
.
(2)由(1)知对称轴![]() ,即
,即![]() ,得
,得![]()
∴![]() ,
,
令![]() ,则
,则![]() ,即
,即![]()
解得![]()
由于点B在点C左侧
∴点C的坐标为![]() .
.
(3)![]() 抛物线
抛物线![]() 与y轴交于点A,
与y轴交于点A,
![]() 点A的坐标为
点A的坐标为![]() .
.
![]() 点M与点A关于抛物线的对称轴对称,
点M与点A关于抛物线的对称轴对称,
![]() 点M的坐标为
点M的坐标为![]() .
.
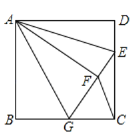
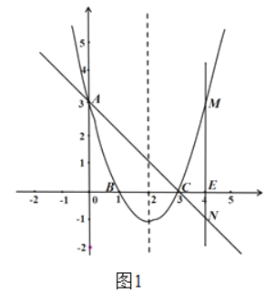
①当![]() 时,如图1.
时,如图1.
![]() 轴,
轴,
![]() ,即
,即![]() .
.
![]() .
.
∴![]()
若![]() ,即
,即![]() ,得
,得![]() .
.
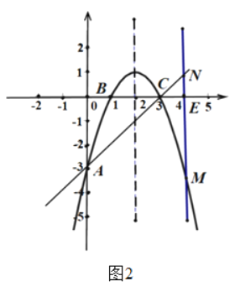
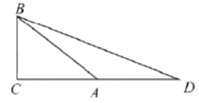
②当![]() 时,如图2.
时,如图2.
同理可得![]()
若![]() ,即
,即![]() ,得
,得![]() .
.
综上所述,a的取值范围是![]() 或
或![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】在某项比赛中,已知不同小组的甲、乙两队的五次预选赛成绩(每次比赛的成绩为0分,10分,20分三种情况)分别如下列不完整的统计表及条形统计图所示.
甲队五次预选赛成绩统计表
比赛场次 | 1 | 2 | 3 | 4 | 5 |
成绩(分) | 20 | 0 | 20 | x | 20 |
乙队五次预选赛成绩条形统计图
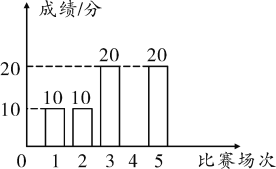
已知甲、乙两队五次预选赛成绩的众数相同,平均数也相同.
(1)求出乙第四次预选赛的成绩;
(2)求甲队成绩的平均数及x的值;
(3)从甲、乙两队前3次比赛中随机各选择一场比赛的成绩进行比较,求选择到的甲队成绩优于乙队成绩的概率.
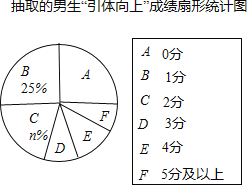
【题目】某市明年的初中毕业升学考试,拟将“引体向上”作为男生体育考试的一个必考项目,满分为10分.有关部门为提前了解明年参加初中毕业升学考试的男生的“引体向上”水平,在全市八年级男生中随机抽取了部分男生,对他们的“引体向上”水平进行测试,并将测试结果绘制成如下统计图表(部分信息未给出):
请你根据统计图表中的信息,解答下列问题:
抽取的男生“引体向上”成绩统计表
成绩 | 人数 |
0分 | 32 |
1分 | 30 |
2分 | 24 |
3分 | 11 |
4分 | 15 |
5分及以上 | m |
(1)填空:m= ,n= .
(2)求扇形统计图中D组的扇形圆心角的度数;
(3)目前该市八年级有男生3600名,请估计其中“引体向上”得零分的人数.