题目内容
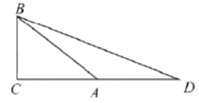
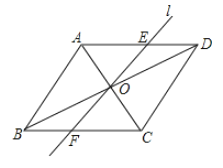
【题目】如图1,扇形![]() 的半径为3,面积为
的半径为3,面积为![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() .
.
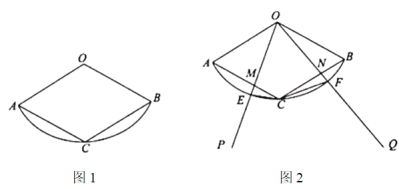
(1)求证:四边形![]() 是菱形;
是菱形;
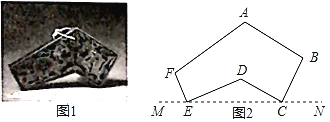
(2)如图2,![]() ,
,![]() 绕点
绕点![]() 旋转,与
旋转,与![]() ,
,![]() 分别交于点
分别交于点![]() (点
(点![]() 与点
与点![]() 均不重合),与
均不重合),与![]() 交于
交于![]() 两点.
两点.
①求![]() 的值;
的值;
②如图2,连接![]() ,
,![]() ,若
,若![]() 的度数是定值,则直接写出
的度数是定值,则直接写出![]() 的度数;若不是,请说明理由.
的度数;若不是,请说明理由.
【答案】(1)证明见解析;(2)①![]() ;②
;②![]() 的度数是定值,为
的度数是定值,为![]() .
.
【解析】
(1)由扇形的面积得出∠AOB=120°,连接OC,证明![]() 与
与![]() 是等边三角形,从而可得结论;
是等边三角形,从而可得结论;
(2)①依据ASA证明![]() ,可得
,可得![]() ,从而可求出
,从而可求出![]() ;
;
②根据已知条件可求出![]() ,由圆周角定理可得
,由圆周角定理可得![]() ,再根据菱形的性质求出∠ACB=120°,最后求出
,再根据菱形的性质求出∠ACB=120°,最后求出![]() 即可.
即可.
(1)证明:如图,连接![]() .
.
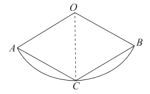
∵![]() ,
,
∴![]() .
.
在扇形![]() 中,
中,![]() ,
,
∵点![]() 是
是![]() 的中点,
的中点,![]() .
.
∴![]() 与
与![]() 是等边三角形,
是等边三角形,
∴![]() .
.
∴四边形![]() 是菱形.
是菱形.
(2)解:如图,
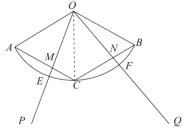
①由(1)可知![]() 与
与![]() 是等边三角形,
是等边三角形,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() ,
,
即![]() .
.
又![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
②![]() 的度数是定值,为
的度数是定值,为![]() .
.
∵![]() ,
,
![]() ,
,![]() ,
,
∴![]() .
.
在菱形![]() 中,
中,![]() ,
,
∴![]() .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
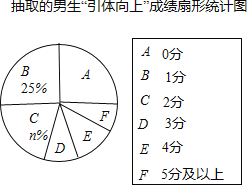
【题目】某市明年的初中毕业升学考试,拟将“引体向上”作为男生体育考试的一个必考项目,满分为10分.有关部门为提前了解明年参加初中毕业升学考试的男生的“引体向上”水平,在全市八年级男生中随机抽取了部分男生,对他们的“引体向上”水平进行测试,并将测试结果绘制成如下统计图表(部分信息未给出):
请你根据统计图表中的信息,解答下列问题:
抽取的男生“引体向上”成绩统计表
成绩 | 人数 |
0分 | 32 |
1分 | 30 |
2分 | 24 |
3分 | 11 |
4分 | 15 |
5分及以上 | m |
(1)填空:m= ,n= .
(2)求扇形统计图中D组的扇形圆心角的度数;
(3)目前该市八年级有男生3600名,请估计其中“引体向上”得零分的人数.