题目内容
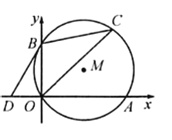
【题目】在平面直角坐标系中,⊙M过坐标原点O且分别交x轴、y轴于点A,B,点C为第一象限内⊙M上一点.若点A(6,0),∠BCO=30°.
(1)求点B的坐标;
(2)若点D的坐标为(-2,0),试猜想直线DB与⊙M的位置关系,并说明理由.
【答案】(1)B(0,2![]() );(2)DB与⊙M相切,理由见解析.
);(2)DB与⊙M相切,理由见解析.
【解析】
(1)连接AB,则AB为⊙M的直径,由圆周角定理可知∠BAO=30°,求出OB的长即可得到点B的坐标;
(2)分别求出DB,DA,AB的长,运用勾股定理逆定理证明△ABD为直角三角形即可.
(1) 如图,连接AB,

∵∠BAO=∠BCO=30°,∠AOB=90°,
∴AB为⊙M的直径,
∵A(6,0),
∴OA=6.
∵tan∠BAO=![]() ,
,
∴OB=2![]() ,
,
∴B(0,2![]() );
);
(2)DB与⊙M相切,理由如下:
∵D(-2,0),OD=2,
∴DB2=OB2+OD2=(2![]() )2+22=12+4=16,
)2+22=12+4=16,
AD2=(OA+OD)2=(6+2)2=64
AB2=OA2+OB2=62+(2![]() )2=48,
)2=48,
∴DB2+AB2=AD2,
∴△ABD为直角三角形,且∠ABD=90°,
即DB与⊙M相切.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
【题目】疫情期间,“线上教学”为我们提供了复习的渠道.学校随机抽取部分学生就“你是否喜欢线上教学”进行了问卷调查,并将调查结果统计后绘制成如下统计表和统计图.
调查结果统计表
类别 | 非常喜欢 | 喜欢 | 一般 | 不喜欢 |
频数 | a | 70 | 20 | 10 |
频率 | 0.5 | b | 0.15 | |
调查结果扇形统计图

(1)在统计表中,a= ;b= ;
(2)在扇形统计图中,对线上教学感觉“一般”所对应的圆心角度数为 ;
(3)已知全校共有3000名学生,试估计“喜欢”线上教学的学生人数.