题目内容
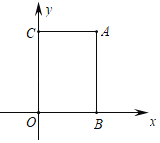
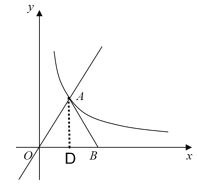
【题目】如图,在平面直角坐标系中,O为坐标原点,正比例函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像都经过点A(2,m).
的图像都经过点A(2,m).
(1)求反比例函数的解析式;
(2)点B在![]() 轴的上,且OA=BA,反比例函数图像上有一点C,且∠ABC=90°,求点C坐标.
轴的上,且OA=BA,反比例函数图像上有一点C,且∠ABC=90°,求点C坐标.

【答案】(1)反比例函数的解析式为:![]() ;(2)点C坐标为(4,
;(2)点C坐标为(4,![]() ).
).
【解析】
(1)将点A坐标代入正比例函数解析式求出m,可得点A的完整坐标,再将点A代入反比例函数的解析式求出k即可;
(2)过点A作AD垂直OB于D,根据等腰三角形三线合一可得OD=BD,求出B点坐标,利用两点间距离公式表示出AB、BC和AC,根据∠ABC=90°利用勾股定理列出方程,解方程即可解决问题.
解:(1)将点A(2,m)代入![]() ,得:
,得:![]() ,
,
∴A(2,![]() ),
),
将点A(2,![]() )代入
)代入![]() 得:
得:![]() ,
,
∴![]() ,
,
∴反比例函数的解析式为:![]() ;
;
(2)过点A作AD垂直OB于D,
∵OA=BA,
∴OD=BD,
∵A(2,![]() ),
),
∴OD=2,
∴OB=4,即B(4,0),
设点C坐标为(a,![]() ),
),
则![]() ,
,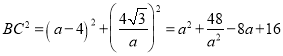 ,
,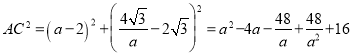 ,
,
∵∠ABC=90°,
∴![]() ,即
,即![]() ,
,
整理得:![]() ,
,
解得:a=4或-3,
经检验,a=4或-3均是分式方程的解,
∵x>0,
∴a=4,
∴点C坐标为(4,![]() ).
).

练习册系列答案
相关题目