题目内容
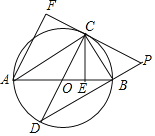
【题目】如图,AB是⊙O的直径,点E为线段OB上一点(不与O,B重合),作EC⊥OB,交⊙O于点C,作直径CD,过点C的切线交DB的延长线于点P,作AF⊥PC于点F,连接CB.
(1)求证:AC平分∠FAB;
(2)求证:BC2=CECP;
(3)当AB=4![]() 且
且![]() =
=![]() 时,求劣弧
时,求劣弧![]() 的长度.
的长度.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】(1)根据已知先证明∠ACF=∠ACE,再根据等角的余角相等即可证得;
(2)只要证明△CBE∽△CPB,可得![]() 即可解决问题;
即可解决问题;
(3)作BM⊥PF于M,则CE=CM=CF,设CE=CM=CF=3a,PC=4a,PM=a,利用相似三角形的性质求出BM,求出tan∠BCM的值即可解决问题;
(1)∵AB是直径,
∴∠ACB=90°,
∴∠BCP+∠ACF=90°,∠ACE+∠BCE=90°,
∵∠BCP=∠BCE,
∴∠ACF=∠ACE,
∵∠AFC=90°,∠AEC=90°,
∴∠FAC=∠EAC,
即AC平分∠FAB;
(2)∵OC=OB,
∴∠OCB=∠OBC,
∵PF是⊙O的切线,CE⊥AB,
∴∠OCP=∠CEB=90°,
∴∠PCB+∠OCB=90°,∠BCE+∠OBC=90°,
∴∠BCE=∠BCP,
∵CD是直径,
∴∠CBD=∠CBP=90°,
∴△CBE∽△CPB,
∴![]() ,
,
∴BC2=CECP;
(3)如图,作BM⊥PF于M.则CE=CM=CF,
设CE=CM=CF=3a,PC=4a,PM=a,
∵∠MCB+∠P=90°,∠P+∠PBM=90°,
∴∠MCB=∠PBM,
∵CD是直径,BM⊥PC,
∴∠CMB=∠BMP=90°,
∴△BMC∽△PMB,
∴![]() ,
,
∴BM2=CMPM=3a2,
∴BM=![]() a,
a,
∴tan∠BCM=![]() ,
,
∴∠BCM=30°,
∴∠OCB=∠OBC=∠BOC=60°,∠BOD=120°,
∴![]() 的长=
的长=![]() .
.