题目内容
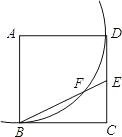
【题目】如图,点E是正方形ABCD的边CD上一点,以A为圆心,AB为半径的弧与BE交于点F,则∠EFD=_____°.
【答案】45
【解析】
由四边形ABCD为正方形及半径相等得到AB=AF=AD,∠ABD=∠ADB=45°,利用等边对等角得到两对角相等,由四边形ABFD的内角和为360度,得到四个角之和为270,利用等量代换得到∠ABF+∠ADF=135°,进而确定出∠1+∠2=45°,由∠EFD为三角形DEF的外角,利用外角性质即可求出∠EFD的度数.
∵正方形ABCD,AF,AB,AD为圆A半径,
∴AB=AF=AD,∠ABD=∠ADB=45°,
∴∠ABF=∠AFB,∠AFD=∠ADF,
∵四边形ABFD内角和为360°,∠BAD=90°,
∴∠ABF+∠AFB+∠AFD+∠ADF=270°,
∴∠ABF+∠ADF=135°,
∵∠ABD=∠ADB=45°,即∠ABD+∠ADB=90°,
∴∠1+∠2=135°90°=45°,
∵∠EFD为△DEF的外角,
∴∠EFD=∠1+∠2=45°.
故答案为:45

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目