题目内容
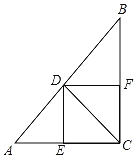
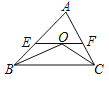
【题目】如图①线段![]() 是
是![]() 的直径,
的直径,![]() 点
点![]() 在
在![]() 上,
上,![]() 点
点![]() 在射线
在射线![]() 上运动(点
上运动(点![]() 不与点
不与点![]() 重合),直径
重合),直径![]() 的垂线
的垂线![]() 与
与![]() 的平行线
的平行线![]() 相交于点
相交于点![]() 连接
连接![]() 设
设![]()
![]() 求
求![]() 的取值范围;
的取值范围;
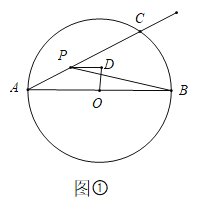
![]() 如图②点
如图②点![]() 是线段
是线段![]() 与
与![]() 的交点,若
的交点,若![]() 求证:直线
求证:直线![]() 与
与![]() 相切;
相切;

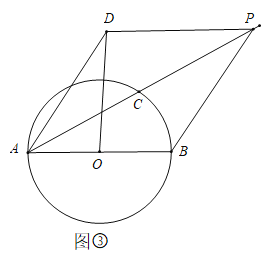
![]() 如图③当
如图③当![]() 时,连接
时,连接![]() 判断四边形
判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
【答案】(1)x≥2;(2)证明见解析;(3)四边形![]() 为菱形,理由见解析.
为菱形,理由见解析.
【解析】
(1)当点P在点C处,PB取得最小值,即x=![]() AB=2,即可求解;
AB=2,即可求解;
(2)若证明线段PD与⊙O相切,可证明![]() 且OD=OA=2,连接
且OD=OA=2,连接![]() 过点
过点![]() 作
作![]() 于点
于点![]() 先求得PH和AP,即可求得OD.
先求得PH和AP,即可求得OD.
(3)先证得![]() ,求得AP和IA,
,求得AP和IA,![]() ,求得
,求得![]() ,故得DP,DP=AB,且
,故得DP,DP=AB,且![]() 可证得四边形
可证得四边形![]() 为平行四边形,又因为
为平行四边形,又因为![]() =PB,所以四边形
=PB,所以四边形![]() 为菱形.
为菱形.
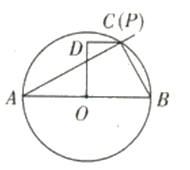
(1)如图所示,当点![]() 与
与![]() 重合时,
重合时,![]() 最短.
最短.
∵![]() 是⊙O的直径,
是⊙O的直径,
∴![]() .
.
∵![]() ,
,
∴![]()
∴![]() .
.
故答案为:![]()
(2)如图所示:连接![]() 过点
过点![]() 作
作![]() 于点
于点![]()
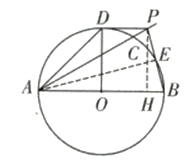
∵![]() 是⊙O的直径,
是⊙O的直径,
∴![]() .
.
∵![]()
∴![]()
∴![]() .
.
在![]() 中,
中,![]()
∴![]() .
.
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴直线![]() 与⊙O相切;
与⊙O相切;
(3)四边形![]() 为菱形.
为菱形.
理由如下:
如图所示:连接![]() 与
与![]() 相交于点
相交于点![]() ,
,
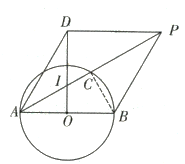
∵![]() 是⊙O的直径
是⊙O的直径
∴![]()
∵![]()
∴![]()
∴![]() .
.
在![]() 中,
中,![]()
∴![]() .
.
∴在![]() 中,
中,![]()
∴![]()
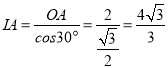
∴![]()
∵![]() ,
,
∴![]()
在![]() 中,
中,![]()
∴![]()
∴![]() .
.
又∵![]()
∴四边形![]() 为平行四边形
为平行四边形
∵![]()
∴四边形![]() 为菱形.
为菱形.

练习册系列答案
相关题目