题目内容
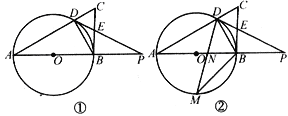
【题目】如图1,在平面直角坐标系xOy中,A(0,4),B(8,0),C(8,4).
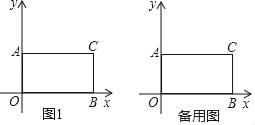
(1)试说明四边形AOBC是矩形.
(2)在x轴上取一点D,将△DCB绕点C顺时针旋转90°得到△D'CB'(点D'与点D对应).
①若OD=3,求点D'的坐标.
②连接AD'、OD',则AD'+OD'是否存在最小值,若存在,请直接写出最小值及此时点D'的坐标;若不存在,请说明理由.
【答案】(1)见解析;(2)①D'的坐标为(4,9),②AD'+OD'的最小值是![]() 或4
或4![]() ,点D'的坐标是(4,2).
,点D'的坐标是(4,2).
【解析】
(1)根据矩形的判定证明即可;
(2)①当点D在原点右侧时,根据旋转的性质和矩形的性质解答即可;②当点D在原点左侧时,根据旋转的性质和矩形的性质解答即可.
(1)∵A(0,4),B(8,0),C(8,4).
∴OA=4,BC=4,OB=8,AC=8,
∴OA=BC,AC=OB,
∴四边形AOBC是平行四边形,
∵∠AOB=90°,
∴AOBC是矩形;
(2)∵AOBC是矩形,
∴∠ACB=90°,∠OBC=90°,
∵△D'CB'将△DCB绕点C顺时针旋转90°得到(点D'与点D对应),
∴∠D'B'C=∠DBC=90°,B'C=BC=4,D'B'=DB,∠BCB'=90°,
即点B'在AC边上,
∴D'B'⊥AC,
①如图1,当点D在原点右侧时:D'B'=DB=8﹣3=5,

∴点D'的坐标为(4,9);
②如图2,当点D在原点左侧时:D'B'=DB=8+3=11,
∴点D'的坐标为(4,15),
综上所述:点D'的坐标为(4,9)或(4,15).
AD'+OD'的最小值是![]() (或4
(或4![]() ),
),
点D'的坐标是(4,2).

【题目】 某公司的一批某品牌衬衣的质量抽检结果如下:
抽检件数 | 50 | 100 | 200 | 300 | 400 | 500 |
次品件数 | 0 | 4 | 16 | 19 | 24 | 30 |
(1)请结合表格数据直接写出这批衬衣中任抽1件是次品的概率.
(2)如果销售这批衬衣600件,至少要准备多少件正品衬衣供买到次品的顾客退换?