题目内容
【题目】如图①,在Rt△ABC中,∠ABC=90o,AB是⊙O的直径,⊙O交AC于点D,过点D的直线交BC于点E,交AB的延长线于点P,∠A=∠PDB.
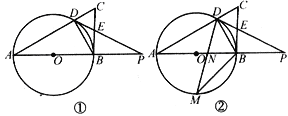
(1)求证:PD是⊙O的切线;
(2)若AB=4,DA=DP,试求弧BD的长;
(3)如图②,点M是弧AB的中点,连结DM,交AB于点N.若tanA=![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)连结OD;由AB是⊙O的直径,得到∠ADB=90°,根据等腰三角形的性质得到∠ADO=∠A,∠BDO=∠ABD;得到∠PDO=90°,且D在圆上,于是得到结论;
(2)设∠A=x,则∠A=∠P=x,∠DBA=2x,在△ABD中,根据∠A+∠ABD=90o列方程求出x的值,进而可得到∠DOB=60o,然后根据弧长公式计算即可;
(3)连结OM,过D作DF⊥AB于点F,然后证明△OMN∽△FDN,根据相似三角形的性质求解即可.
(1)连结OD,∵AB是⊙O的直径,∴∠ADB=90o,
∠A+∠ABD=90o,又∵OA=OB=OD,∴∠BDO=∠ABD,
又∵∠A=∠PDB,∴∠PDB+∠BDO=90o,即∠PDO=90o,
且D在圆上,∴PD是⊙O的切线.
(2)设∠A=x,
∵DA=DP,∴∠A=∠P=x,∴∠DBA=∠P+∠BDP=x+x=2x,
在△ABD中,
∠A+∠ABD=90o,x=2x=90o,即x=30o,
∴∠DOB=60o,∴弧BD长![]() .
.
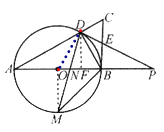
(3)连结OM,过D作DF⊥AB于点F,∵点M是![]() 的中点,
的中点,
∴OM⊥AB,设BD=x,则AD=2x,AB=![]() =2OM,即OM=
=2OM,即OM=![]() ,
,
在Rt△BDF中,DF=![]() ,
,
由△OMN∽△FDN得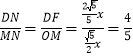 .
.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目