题目内容
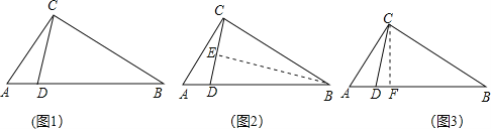
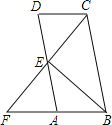
【题目】如图,四边形ABCD中,CD∥AB,E是AD中点,CE交BA延长线于点F.
(1)试说明:CD=AF;
(2)若BC=BF,试说明:BE⊥CF.
【答案】(1)证明见解析;(2)证明见解析
【解析】
(1)由CD∥AB,可得∠CDE=∠FAE,而E是AD中点,因此有DE=AE,再有∠AEF=∠DEC,所以利用ASA可证△CDE≌△FAE,再利用全等三角形的性质,可得CD=AF;
(2)先利用(1)中的三角形的全等,可得CE=FE,再根据BC=BF,利用等腰三角形三线合一的性质,可证BE⊥CF.
证明:(1)∵CD∥AB,
∴∠CDE=∠FAE,
又∵E是AD中点,
∴DE=AE,
又∵∠AEF=∠DEC,
∴△CDE≌△FAE,
∴CD=AF;
(2)∵BC=BF,
∴△BCF是等腰三角形,
又∵△CDE≌△FAE,
∴CE=FE,
∴BE⊥CF(等腰三角形底边上的中线与底边上的高相互重合).

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目