题目内容
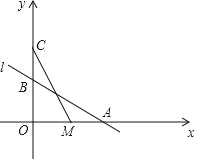
【题目】如图,直线l:y=﹣![]() x+2与x轴,y轴分別交于点A,B,在y轴上有一点C(0,4),动点M从点A出发以毎秒1个単位长度的速度沿x轴向左运动,设运动的时间为t秒.
x+2与x轴,y轴分別交于点A,B,在y轴上有一点C(0,4),动点M从点A出发以毎秒1个単位长度的速度沿x轴向左运动,设运动的时间为t秒.
(1)求点A的坐标;
(2)请从A,B两题中任选一题作答.
A.求△COM的面积S与时间t之间的函数表达式;
B.当△ABM为等腰三角形时,求t的值.
【答案】(1)A(4,0)、B(0,2)(2)A、当0≤t≤4时,8﹣2t;当t>4时,2t﹣8;B、![]() s或2
s或2![]() s或8s.
s或8s.
【解析】
(1)由直线L的函数解析式,令y=0求A点坐标,x=0求B点坐标;
(2)A、由面积公式S=![]() OMOC求出S与t之间的函数关系式;
OMOC求出S与t之间的函数关系式;
B、△ABM是等腰三角形,有三种情形,分别求解即可.
(1)对于直线AB:y=﹣![]() x+2,
x+2,
当x=0时,y=2,
当y=0时,x=4,
则A、B两点的坐标分别为A(4,0)、B(0,2);
(2)A、∵C(0,4),A(4,0),
∴OC=OA=4,
当0≤t≤4时,OM=OA﹣AM=4﹣t,S△OCM=![]() ×4×(4﹣t)=8﹣2t;
×4×(4﹣t)=8﹣2t;
当t>4时,OM=AM﹣OA=t﹣4,S△OCM=![]() ×4×(t﹣4)=2t﹣8;
×4×(t﹣4)=2t﹣8;
B、△ABM是等腰三角形,有三种情形:
①当BM=AM时,设BM=AM=x,则OM=4﹣x,
在Rt△OBM中,∵OB2+OM2=BM2,
∴22+(4﹣x)2=x2,
∴x=![]() ,
,
∴AM=![]() ,
,
∴t=![]() 时,△ABM是等腰三角形;
时,△ABM是等腰三角形;
②当AM′=AB=![]() =2
=2![]() 时,即t=2
时,即t=2![]() 时,△ABM是等腰三角形;
时,△ABM是等腰三角形;
③当BM″=BA时,∵OB⊥AM″,
∴OM″=OA=4,
∴AM″=8,
∴t=8时,△ABM是等腰三角形,
综上所述,满足条件的t的值为![]() s或2
s或2![]() s或8s.
s或8s.

【题目】一辆汽车在公路上匀速行驶,下表记录的是汽车在加满油后油箱内余油量y(升)与行驶时间x(时)之间的关系:
行驶时间x(时) | 0 | 1 | 2 | 2.5 |
余油量y(升) | 100 | 80 | 60 | 50 |
(1)小明分析上表中所给的数据发现x,y成一次函数关系,试求出它们之间的函数表达式(不要求写出自变量的取值范围);
(2)求汽车行驶4.2小时后,油箱内余油多少升?