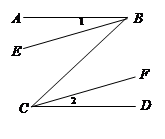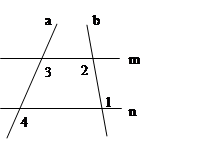题目内容
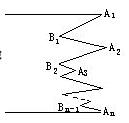
如图,AA1∥BA2,过B1 作AA1的平行线中,则∠A1、∠A1B1A2、∠A2之间的数量关系为_______,如图所示当AA1∥BAn.则∠A1、∠A2、…∠An、与∠B1、∠B2…∠Bn-1的数量关系为_____________________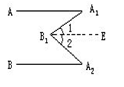


∠A1B1A2=∠A1+∠A2,∠A1+∠A2+…+∠An、=∠B1+∠B2 +…+∠Bn-1
试题分析:根据平行线的性质可得∠A1=∠1,∠A2=∠2,即可得到∠A1、∠A1B1A2、∠A2之间的数量关系,再运用这个特征求解即可.
∵AA1∥BA2
∴∠A1=∠1,∠A2=∠2
∵∠A1B1A2=∠1+∠1
∴∠A1B1A2=∠A1+∠A2
∴∠A1+∠A2+…+∠An、=∠B1+∠B2 +…+∠Bn-1.
点评:平行线的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中半径常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
相关题目
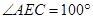 ,则
,则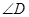 等于( )
等于( )