题目内容
填空完成下列推理过程
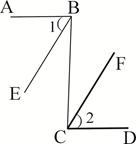
如图,已知AB⊥BC,BC⊥CD,
∠1=∠2,试判断BE与CF的关系,并说明理由。
解:
理由:∵AB⊥BC,BC⊥CD(已知)
∴ = =90°( )
∵∠1=∠2( )
∴∠ABC-∠1=∠BCD-∠2
即∠EBC=∠BCF
∴ ∥ ( )

如图,已知AB⊥BC,BC⊥CD,
∠1=∠2,试判断BE与CF的关系,并说明理由。
解:
理由:∵AB⊥BC,BC⊥CD(已知)
∴ = =90°( )
∵∠1=∠2( )
∴∠ABC-∠1=∠BCD-∠2
即∠EBC=∠BCF
∴ ∥ ( )
BE//CF,∠ABC, ∠BCD,(垂直定义);(已知);BE//CF(内错角相等,两直线平行)
试题分析:根据垂直的定义可得∠ABC=∠BCD=90°,再结合∠1=∠2可得∠EBC=∠BCF,最后根据内错角相等,两直线平行即可证得结论.
BE//CF
理由:∵AB⊥BC,BC⊥CD(已知)
∴∠ABC=∠BCD=90°(垂直定义)
∵∠1=∠2(已知)
∴∠ABC-∠1=∠BCD-∠2
即∠EBC=∠BCF
∴BE//CF(内错角相等,两直线平行).
点评:本题属于基础应用题,只需学生熟练掌握垂直的定义及平行线的判定方法,即可完成.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
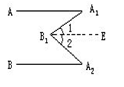
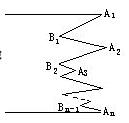



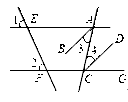
 ∠EAC,∠4=
∠EAC,∠4=
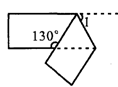
 ,则∠2的大小是( )
,则∠2的大小是( )