题目内容
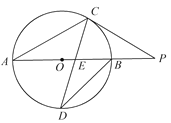
【题目】如图，OA、OB是⊙O的两条半径，OA⊥OB，C是半径OB上一动点，连接AC并延长交⊙O于D，过点D作圆的切线交OB的延长线于E，已知OA＝6．
（1）求证：∠ECD＝∠EDC；
（2）若BC＝2OC，求DE长；
（3）当∠A从15°增大到30°的过程中，求弦AD在圆内扫过的面积．
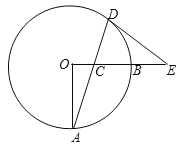
【答案】（1）证明见解析；（2）8；（3）
.
【解析】
（1）连接OD，由切线的性质得出∠EDC+∠ODA=90°，由等腰三角形的性质得出∠ODA=∠OAC，得出∠EDC=∠ACO，即可得出结论；
（2）设DE=x，则CE=DE=x，OE=2+x，在Rt△ODE中，由勾股定理得出方程，解法长即可；
（3）过点D作DF⊥AO交AO的延长线于F，当∠A=15°时，∠DOF=30°，得出DF=
OD=OA=3，∠DOA=150°，S弓形ABD=S扇形ODA-S△AOD=15π-9，当∠A=30°时，∠DOF=60°，S弓形ABD=S扇形ODA-S△AOD=12π-9
，即可得出结果．
（1）证明：连接OD，如图1所示：
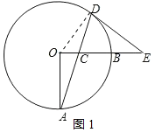
∵DE是⊙O的切线，
∴∠EDC+∠ODA＝90°，
∵OA⊥OB，
∴∠ACO+∠OAC＝90°，
∵OA、OB是⊙O的两条半径，
∴OA＝OB，
∴∠ODA＝∠OAC，
∴∠EDC＝∠ACO，
∵∠ECD＝∠ACO，
∴∠ECD＝∠EDC；
（2）∵BC＝2OC，OB＝OA＝6，
∴OC＝2，
设DE＝x，
∵∠ECD＝∠EDC，
∴CE＝DE＝x，
∴OE＝2+x，
∵∠ODE＝90°，
∴OD2+DE2＝OE2，
即：62+x2＝（2+x）2，
解得：x＝8，
∴DE＝8；
（3）解：过点D作DF⊥AO交AO的延长线于F，如图2所示：
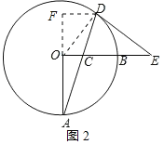
当∠A＝15°时，∠DOF＝30°，
∴DF＝OD＝OA＝3，∠DOA＝150°，
S弓形ABD＝S扇形ODA﹣S△AOD＝
﹣OADF＝15π﹣×6×3＝15π﹣9，
当∠A＝30°时，∠DOF＝60°，
∴DF＝
OD＝OA＝3，∠DOA＝120°，
S弓形ABD＝S扇形ODA﹣S△AOD＝
﹣OADF＝12π﹣×6×3＝12π﹣9，
∴当∠A从15°增大到30°的过程中，AD在圆内扫过的面积＝（15π﹣9）﹣（12π﹣9）＝3π+9﹣9．
