题目内容
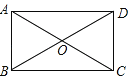
【题目】已知矩形ABCD,作∠ABC的平分线交AD边于点M,作∠BMD的平分线交CD边于点N.
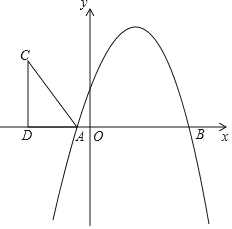
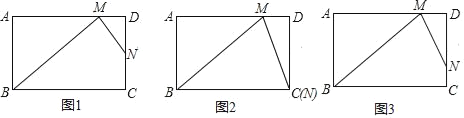
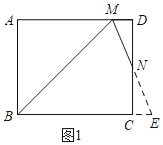
(1)若N为CD的中点,如图1,求证:BM=AD+DM;
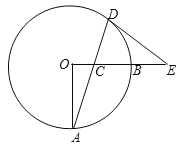
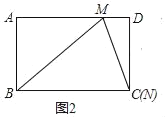
(2)若N与C点重合,如图2,求tan∠MCD的值;
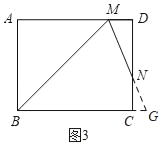
(3)若![]() ,AB=6,如图3,求BC的长.
,AB=6,如图3,求BC的长.
【答案】(1)详见解析;(2)![]() ;
;
【解析】
(1)如图1,作辅助线,构建全等三角形,证明△DNM≌△CNE(AAS),得DM=CE,证明∠BMN=∠E=67.5°,可得结论;
(2)如图2,当N与C重合时,BC=BM,设AB=x,则BM=BC=![]() x,表示DM的长,根据三角函数定义可得结论;
x,表示DM的长,根据三角函数定义可得结论;
(3)如图3,延长MN、BC交于点G,根据等腰直角三角形定义可得BM的长,即是BG的长,设CG=m,则DM=2m,表示BC的长,列方程可得结论.
(1)证明:如图1,延长MN、BC交于点E,
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,∠ABC=90°,
∴∠D=∠NCE,∠DMN=∠NEC,
∵N是DC的中点,
∴DN=CN,
∴△DNM≌△CNE(AAS),
∴DM=CE,
∵BM平分∠ABC,∠ABC=90°,
∴∠ABM=∠MBE=45°,
∵AD∥BC,
∴∠AMB=∠EBM=45°,
∴∠BMD=180°﹣45°=135°,
∵MN平分∠BMD,
∴∠BMN=∠DMN=67.5°,
∴∠E=∠DMN=67.5°,
∴∠BMN=∠E=67.5°,
∴BM=BE=BC+CE=AD+DM;
(2)解:如图2,当N与C重合时,
由(1)知:∠BMC=∠DMN=∠BCM,
∴BC=BM,
设AB=x,则BM=BC=![]() x,
x,
∵AD=BC,
∴DM=![]() x﹣x,
x﹣x,
Rt△DMC中,tan∠MCD=![]() ;
;
(3)解:如图3,延长MN、BC交于点G,
∵四边形ABCD是矩形,
∴CD=AB=6,
∵![]() ,
,
∴CN=2,DN=4,
∵△ABM是等腰直角三角形,
∴BM=6![]() ,
,
由(1)知:BM=BG=6![]() ,
,
∵DM∥CG,
∴△DMN∽△CGN,
∴![]() ,
,
设CG=m,则DM=2m,
6![]() =6+2m+m,
=6+2m+m,
m=2![]() ﹣2,
﹣2,
∴BC=6+2m=2+4![]() .
.