题目内容

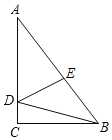
【题目】在Rt△ABC中，∠ACB=90°，AC=8，BC=6，点D、E分别在AC、AB上，且△ADE是直角三角形，△BDE是等腰三角形，则BE=_________.

【答案】或．

【解析】

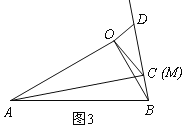
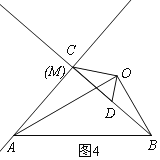
分两种情形：①如图1中，当∠AED=90°，DE=BE时．②如图2中，当∠ADE=90°，DE=EB时．利用相似三角形的性质，构建方程即可解决问题

①如图1中，当∠AED=90°，DE=BE时，设DE=BE=x．

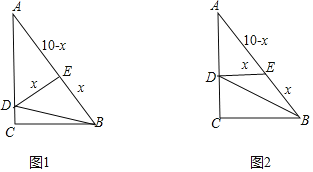
在Rt△ABC中，∵AC=8，BC=6，

∴AB==10，

∵∠A=∠A，∠AED=∠C=90°，

∴△AED∽△ACB，

∴，

∴，

解得x=．

②如图2中，当∠ADE=90°，DE=EB时，设DE=BE=x，

∵△ADE∽△ACB，

∴，

∴，

解得x=，

综上所述，BE的值为或．

练习册系列答案
相关题目

【题目】如图，C是以AB为直径的半圆O上一点，连结AC，BC，分别以AC，BC为边向外作正方形ACDE，BCFG，DE，FG, 的中点分别是M，N，P，Q．若MP+NQ＝14，AC+BC＝20，则AB的长是（　　）

A. 9B. C. 13D. 16

【题目】如图，抛物线y＝﹣x2+bx+c与x轴分别交于A（﹣1，0），B（5，0）两点．

（1）求抛物线的解析式；

（2）在第二象限内取一点C，作CD垂直x轴于点D，连接AC，且AD＝5，CD＝8，将Rt△ACD沿x轴向右平移m个单位，当点C落在抛物线上时，求m的值．

【题目】（1）问题发现

如图1，在△OAB和△OCD中，OA=OB，OC=OD，∠AOB=∠COD=40°，连接AC，BD交于点M．填空：

①的值为　 　；

②∠AMB的度数为　 　．

（2）类比探究

如图2，在△OAB和△OCD中，∠AOB=∠COD=90°，∠OAB=∠OCD=30°，连接AC交BD的延长线于点M．请判断的值及∠AMB的度数，并说明理由；

（3）拓展延伸

在（2）的条件下，将△OCD绕点O在平面内旋转，AC，BD所在直线交于点M，若OD=1，OB=，请直接写出当点C与点M重合时AC的长．

【答案】（1）①1；②40°；（2），90°；（3）AC的长为3或2．

【解析】

（1）①证明△COA≌△DOB（SAS），得AC=BD，比值为1；

②由△COA≌△DOB，得∠CAO=∠DBO，根据三角形的内角和定理得：∠AMB=180°-（∠DBO+∠OAB+∠ABD）=180°-140°=40°；

（2）根据两边的比相等且夹角相等可得△AOC∽△BOD，则，由全等三角形的性质得∠AMB的度数；

（3）正确画图形，当点C与点M重合时，有两种情况：如图3和4，同理可得：△AOC∽△BOD，则∠AMB=90°，，可得AC的长．

（1）问题发现：

①如图1，

∵∠AOB=∠COD=40°，

∴∠COA=∠DOB，

∵OC=OD，OA=OB，

∴△COA≌△DOB（SAS），

∴AC=BD，

∴

②∵△COA≌△DOB，

∴∠CAO=∠DBO，

∵∠AOB=40°，

∴∠OAB+∠ABO=140°，

在△AMB中，∠AMB=180°-（∠CAO+∠OAB+∠ABD）=180°-（∠DBO+∠OAB+∠ABD）=180°-140°=40°，

（2）类比探究：

如图2，，∠AMB=90°，理由是：

Rt△COD中，∠DCO=30°，∠DOC=90°，

∴，

同理得：，

∴，

∵∠AOB=∠COD=90°，

∴∠AOC=∠BOD，

∴△AOC∽△BOD，

∴ ，∠CAO=∠DBO，

在△AMB中，∠AMB=180°-（∠MAB+∠ABM）=180°-（∠OAB+∠ABM+∠DBO）=90°；

（3）拓展延伸：

①点C与点M重合时，如图3，

同理得：△AOC∽△BOD，

∴∠AMB=90°，，

设BD=x，则AC=x，

Rt△COD中，∠OCD=30°，OD=1，

∴CD=2，BC=x-2，

Rt△AOB中，∠OAB=30°，OB=，

∴AB=2OB=2，

在Rt△AMB中，由勾股定理得：AC2+BC2=AB2，

(x)2+(x2)2＝(2)2，

x2-x-6=0，

（x-3）（x+2）=0，

x1=3，x2=-2，

∴AC=3；

②点C与点M重合时，如图4，

同理得：∠AMB=90°，，

设BD=x，则AC=x，

在Rt△AMB中，由勾股定理得：AC2+BC2=AB2，

(x)2+（x+2）2=(2)2.

x2+x-6=0，

（x+3）（x-2）=0，

x1=-3，x2=2，

∴AC=2；.

综上所述，AC的长为3或2．

点睛：本题是三角形的综合题，主要考查了三角形全等和相似的性质和判定，几何变换问题，解题的关键是能得出：△AOC∽△BOD，根据相似三角形的性质，并运用类比的思想解决问题，本题是一道比较好的题目．

【题型】解答题
【结束】
25

【题目】如图，已知抛物线y＝ax2+bx﹣3（a≠0）经过点A（3，0），B（﹣1，0）．

（1）求该抛物线的解析式；

（2）若以点A为圆心的圆与直线BC相切于点M，求切点M的坐标；

（3）若点Q在x轴上，点P在抛物线上，是否存在以点B，C，Q，P为顶点的四边形是平行四边形？若存在，直接写出点P的坐标；若不存在，请说明理由．

【题目】一次函数y=kx﹣1的图象经过点P，且y的值随x值的增大而增大，则点P的坐标可以为（　　）

A. （﹣5，3） B. （1，﹣3） C. （2，2） D. （5，﹣1）

【题目】如图，正方形ABCD的顶点A（1，1），B（3，1），规定把正方形ABCD“先沿x轴翻折，再向左平移1个单位”为一次变换，这样连续经过2019次变换后，正方形ABCD的顶点C的坐标为（　　）

A. （﹣2018，3）B. （﹣2018，﹣3）

C. （﹣2016，3）D. （﹣2016，﹣3）

【题目】如图，OA、OB是⊙O的两条半径，OA⊥OB，C是半径OB上一动点，连接AC并延长交⊙O于D，过点D作圆的切线交OB的延长线于E，已知OA＝6．

（1）求证：∠ECD＝∠EDC；

（2）若BC＝2OC，求DE长；

（3）当∠A从15°增大到30°的过程中，求弦AD在圆内扫过的面积．

【题目】（本题满分8分）

为了加强学生课外阅读，开阔视野，某校开展了“书香校园，从我做起”的主题活动．学校随机抽取了部分学生，对他们一周的课外阅读时间进行调查，绘制出频数分布表和频数分布直方图的一部分如下：

请根据图表信息回答下列问题：

（1）频数分布表中的 ， ；

（2）将频数分布直方图补充完整；

（3）学校将每周课外阅读时间在小时以上的学生评为“阅读之星”，请你估计该校名学生中评为“阅读之星”的有多少人？

【题目】某班6个合作小组的人数分别是4，6，4，5，7，8，现第4小组调出1人去第2小组，则新各组人数分别为：4，7，4，4，7，8，下列关于调配后的数据说法正确的是（　　）

A. 调配后平均数变小了B. 调配后众数变小了

C. 调配后中位数变大了D. 调配后方差变大了

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网