题目内容
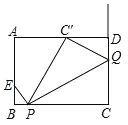
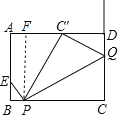
【题目】 如图，在矩形ABCD中，AB＝3，BC＝4，点E是边AB上一点，且AE＝2EB，点P是边BC上一动点，连接EP，过点P作PQ⊥PE交射线CD于点Q．若点C关于直线PQ的对称点恰好落在边AD上，则BP的长为_____．
【答案】1或
【解析】
过点P作 PF⊥AD于点F，可证得四边形CPFD是矩形，可证得△BEP∽△CPQ和△PFC'∽△C'DQ，从而得
，
，可设设BP=x，则DF=PC=4-x，可求得CQ，继而可求得C'D，FC'与BP的关系，而DF=C'D+FC'，通过解一元二次方程，解得x，即可求得BP．
如图，过点P作 PF⊥AD于点F
∴∠PFC＝90°
∵矩形ABCD中，AB＝3，BC＝4
∴∠FAB＝∠B＝∠C＝∠QDC'＝90°，CD＝AB＝3
∴四边形CPFD是矩形
∴DF＝PC，PF＝CD＝3
∵AE＝2EB
∴AE＝2，EB＝1
设BP＝x，则DF＝PC＝4﹣x
∵点C与C'关于直线PQ对称
∴△PC'Q≌△PCQ
∴PC'＝PC＝4﹣x，C'Q＝CQ，∠PC'Q＝∠C＝90°
∵PE⊥PQ
∴∠BPE+∠CPQ＝90°
∵∠BEP+∠BPE＝90°
∴∠BPE＝∠CPQ
∴△BEP∽△CPQ
同理可得：△PFC'∽△C'DQ
∴，，
∴CQ＝
＝x（4﹣x）
∴C'Q＝x（4﹣x），DQ＝3﹣x（4﹣x）＝x2﹣4x+3
∴
∴C'D＝3x，FC′＝
∵FC'+C'D＝DF
∴+3x＝4﹣x
解得x＝1或x＝
故答案为1或
练习册系列答案
相关题目
